题目内容
已知椭圆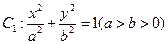 的离心率为
的离心率为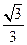 ,直线
,直线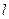 :
: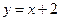 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆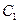 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(I)求椭圆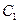 的方程;
的方程;
(II)设椭圆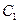 的左焦点为
的左焦点为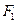 ,右焦点
,右焦点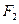 ,直线
,直线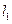 过点
过点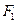 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线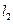 垂直
垂直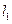 于点
于点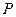 ,线段
,线段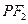 垂直平分线交
垂直平分线交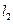 于点
于点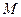 ,求点
,求点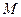 的轨迹
的轨迹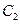 的方程;
的方程;
(III)设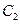 与
与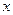 轴交于点
轴交于点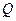 ,不同的两点
,不同的两点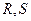 在
在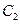 上,且满足
上,且满足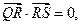 求
求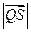 的取值范围.
的取值范围.
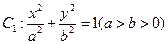 的离心率为
的离心率为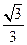 ,直线
,直线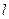 :
: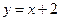 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆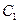 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.(I)求椭圆
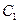 的方程;
的方程;(II)设椭圆
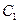 的左焦点为
的左焦点为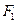 ,右焦点
,右焦点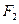 ,直线
,直线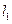 过点
过点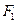 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线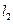 垂直
垂直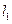 于点
于点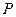 ,线段
,线段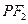 垂直平分线交
垂直平分线交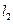 于点
于点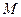 ,求点
,求点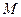 的轨迹
的轨迹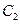 的方程;
的方程;(III)设
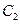 与
与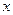 轴交于点
轴交于点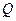 ,不同的两点
,不同的两点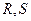 在
在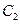 上,且满足
上,且满足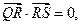 求
求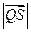 的取值范围.
的取值范围.(Ⅰ)∵
∵直线 相切,
相切,
∴ ∴
∴ …………3分
…………3分
∵椭圆C1的方程是 ………………6分
………………6分
(Ⅱ)∵MP=MF2,
∴动点M到定直线 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为 …………9分
…………9分
(Ⅲ)Q(0,0),设
∴
∵
∴
∵ ,化简得
,化简得
∴ ………………11分
………………11分
∴
当且仅当 时等号成立 …………13分
时等号成立 …………13分
∵
∴当 的取值范围是
的取值范围是 ……14分
……14分

∵直线
 相切,
相切,∴
 ∴
∴ …………3分
…………3分∵椭圆C1的方程是
 ………………6分
………………6分(Ⅱ)∵MP=MF2,
∴动点M到定直线
 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为
 …………9分
…………9分(Ⅲ)Q(0,0),设

∴

∵

∴

∵
 ,化简得
,化简得∴
 ………………11分
………………11分∴

当且仅当
 时等号成立 …………13分
时等号成立 …………13分∵

∴当
 的取值范围是
的取值范围是 ……14分
……14分同答案

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
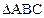 的三个顶点是
的三个顶点是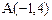 ,
,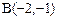 ,
,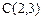 .
. 的线段
的线段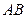 的端点
的端点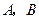 在抛物线
在抛物线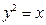 上移动,求
上移动,求 轴距离的最小值,并求出此时
轴距离的最小值,并求出此时

 B
B 
 D
D 
 x上时,求直线AB的方程.
x上时,求直线AB的方程.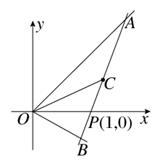
 的倾斜角为
的倾斜角为 ,则
,则 ___________.
___________.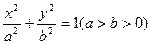 的焦点F(c, 0)的弦中最短弦长是 ( )
的焦点F(c, 0)的弦中最短弦长是 ( )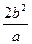
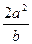
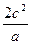
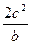
 与曲线
与曲线 (
( )关于直线
)关于直线 对称,则直线
对称,则直线



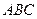 的重心
的重心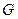 任作一直线分别交
任作一直线分别交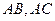 于
于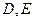 ,
,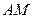 为中线
为中线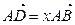 ,
,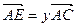 ,
,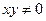 ,求
,求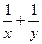 的值
的值