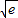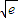题目内容
若直线y=ax与曲线y=lnx相切，则常数a=（ ）
| A．e | B．1 | C．e-1 | D．
|
∵y=lnx，
∴y'=
，
设切点为（m，lnm），得切线的斜率为：
，
所以曲线在点（m，lnm）处的切线方程为：
y-lnm=
×（x-m）．
由题设知它过原点（0，0），∴0-lnm=-1，∴m=e，
∴a=e-1．
故选C．
∴y'=
| 1 |
| x |
设切点为（m，lnm），得切线的斜率为：
| 1 |
| m |
所以曲线在点（m，lnm）处的切线方程为：
y-lnm=
| 1 |
| m |
由题设知它过原点（0，0），∴0-lnm=-1，∴m=e，
∴a=e-1．
故选C．
练习册系列答案
相关题目
