题目内容
在区间(0,1)内随机地取两个数,则这两个之和小于1.5的概率为( )
分析:设取出的两个数为x、y,则可得“0<x<1,0<y<1”表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,而x+y<1.5表示的区域为直线x+y=1.5下方,且在0<x<1,0<y<1所表示区域内部的部分,分别计算其面积,由几何概型的计算公式可得答案
解答: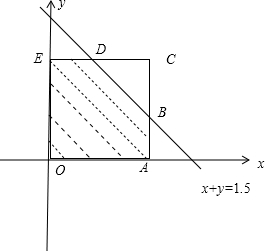 解:设取出的两个数为x、y
解:设取出的两个数为x、y
则有0<x<1,0<y<1,其表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,
而x+y<1.5表示的区域为直线x+y=1.5下方,且在0<x<1,0<y<1表示区域内部的部分
易得其面积为1-
=
则两数之和小于1.5的概率是
故选A
 解:设取出的两个数为x、y
解:设取出的两个数为x、y则有0<x<1,0<y<1,其表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,
而x+y<1.5表示的区域为直线x+y=1.5下方,且在0<x<1,0<y<1表示区域内部的部分
易得其面积为1-
| 1 |
| 8 |
| 7 |
| 8 |
则两数之和小于1.5的概率是
| 7 |
| 8 |
故选A
点评:本题考查几何概型的计算,解题的关键在于用平面区域表示出题干的代数关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本题满分12分)探究函数 的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
|
x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
|
y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知:函数 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:
(1)函数 在区间
上递增.当
在区间
上递增.当 时,
时, ;
;
(2)函数 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
探究函数f(x)=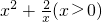 的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
| x | … | 0.25 | 0.5 | 0.75 | 1 | 1.1 | 1.2 | 1.5 | 2 | 3 | 5 | … |
| y | … | 8.063 | 4.25 | 3.229 | 3 | 3.028 | 3.081 | 3.583 | 5 | 9.667 | 25.4 | … |
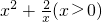 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:(1)函数f(x)=
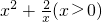 在区间________上递增.当x=________时,y最小=________;
在区间________上递增.当x=________时,y最小=________;(2)函数
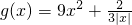 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
探究函数f(x)= 的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
已知:函数f(x)= 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:
(1)函数f(x)= 在区间______上递增.当x=______时,y最小=______;
在区间______上递增.当x=______时,y最小=______;
(2)函数 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
 的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.| x | … | 0.25 | 0.5 | 0.75 | 1 | 1.1 | 1.2 | 1.5 | 2 | 3 | 5 | … |
| y | … | 8.063 | 4.25 | 3.229 | 3 | 3.028 | 3.081 | 3.583 | 5 | 9.667 | 25.4 | … |
 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:(1)函数f(x)=
 在区间______上递增.当x=______时,y最小=______;
在区间______上递增.当x=______时,y最小=______;(2)函数
 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明) ,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下: 
 在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______;
在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______; 有最______值为______,此时x=______;
有最______值为______,此时x=______;  在区间(0,2)上递减;
在区间(0,2)上递减;