题目内容
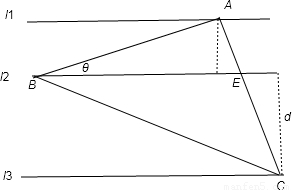
如图11,12,13是同一平面内的三条平行直线,11与12间的距离是2,12与l3间的距离是4.三角形ABC的三个顶点分别在l1、l2、l3上,且三边AB,BC,AC的长之比为1:2: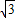 则△ABC的边长AC是( )
则△ABC的边长AC是( )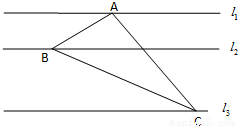
A.4
B.
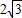
C.
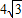
D.
【答案】分析:由题意可设三边长度分别为AB=x,BC=2x,AC=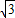 x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC
x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC
解答:解:由题意可设三边长度分别为AB=x,BC=2x,AC=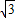 x,(x>0),设AC与l2的交点为E
x,(x>0),设AC与l2的交点为E
∵AB2+AC2=BC2,
∴AB⊥AC即°∠ABC=90,且∠ACB=30°,∠ABC=60°
设∠ABE=θ,∠CBE=60°-θ
又∵sinθ=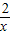 ,
,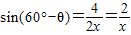
∴sinθ=sin(60°-θ),则有θ=30°
∴AE=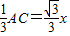 ,EC=
,EC=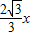 =BE
=BE
在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE
即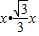 =
=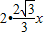
∴x=4,AC=4
故选C.
点评:本题考查直角三角形中的边角关系,两角差的正弦公式的应用,以及求两平行线间的距离的方法.
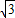 x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC
x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC解答:解:由题意可设三边长度分别为AB=x,BC=2x,AC=
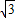 x,(x>0),设AC与l2的交点为E
x,(x>0),设AC与l2的交点为E∵AB2+AC2=BC2,
∴AB⊥AC即°∠ABC=90,且∠ACB=30°,∠ABC=60°
设∠ABE=θ,∠CBE=60°-θ
又∵sinθ=
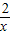 ,
,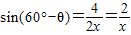
∴sinθ=sin(60°-θ),则有θ=30°
∴AE=
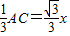 ,EC=
,EC=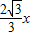 =BE
=BE在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE
即
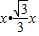 =
=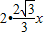
∴x=4,AC=4

故选C.

点评:本题考查直角三角形中的边角关系,两角差的正弦公式的应用,以及求两平行线间的距离的方法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
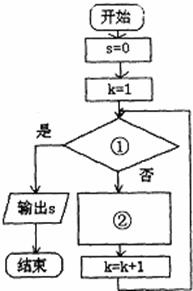 如图是求
如图是求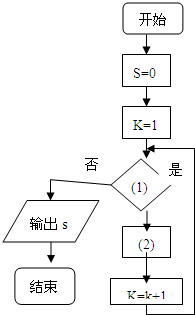 求
求 如图11,12,13是同一平面内的三条平行直线,11与12间的距离是2,12与l3间的距离是4.三角形ABC的三个顶点分别在l1、l2、l3上,且三边AB,BC,AC的长之比为1:2:
如图11,12,13是同一平面内的三条平行直线,11与12间的距离是2,12与l3间的距离是4.三角形ABC的三个顶点分别在l1、l2、l3上,且三边AB,BC,AC的长之比为1:2: 如图是求
如图是求