题目内容
已知集合P=[ ,2],函数y=log2(ax2﹣2x+2)的定义域为Q.
,2],函数y=log2(ax2﹣2x+2)的定义域为Q.
(1)若P∩Q≠Φ,求实数a的取值范围;
(2)若方程log2(ax2﹣2x+2)=2在[ ,2]内有解,求实数a的取值范围.
,2]内有解,求实数a的取值范围.
 ,2],函数y=log2(ax2﹣2x+2)的定义域为Q.
,2],函数y=log2(ax2﹣2x+2)的定义域为Q.(1)若P∩Q≠Φ,求实数a的取值范围;
(2)若方程log2(ax2﹣2x+2)=2在[
 ,2]内有解,求实数a的取值范围.
,2]内有解,求实数a的取值范围.解:(1)若P∩Q≠Φ,则在[ ,2]内至少存在一个x使ax2﹣2x+2>0成立,
,2]内至少存在一个x使ax2﹣2x+2>0成立,
即a>﹣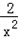 +
+ =﹣2(
=﹣2( ﹣
﹣ )2+
)2+ ∈[﹣4,
∈[﹣4, ],
],
∴a>﹣4
(2)方程log2(ax2﹣2x+2)=2在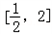 内有解,则ax2﹣2x﹣2=0在
内有解,则ax2﹣2x﹣2=0在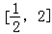 内有解,
内有解,
即在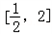 内有值使
内有值使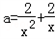 成立,
成立,
设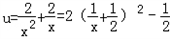 ,当
,当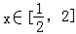 时,
时,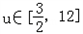 ,
,
∴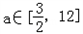 ,
,
∴a的取值范围是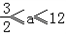 .
.
 ,2]内至少存在一个x使ax2﹣2x+2>0成立,
,2]内至少存在一个x使ax2﹣2x+2>0成立, 即a>﹣
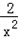 +
+ =﹣2(
=﹣2( ﹣
﹣ )2+
)2+ ∈[﹣4,
∈[﹣4, ],
],∴a>﹣4
(2)方程log2(ax2﹣2x+2)=2在
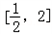 内有解,则ax2﹣2x﹣2=0在
内有解,则ax2﹣2x﹣2=0在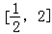 内有解,
内有解,即在
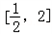 内有值使
内有值使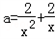 成立,
成立,设
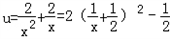 ,当
,当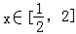 时,
时,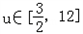 ,
,∴
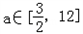 ,
,∴a的取值范围是
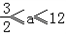 .
.
练习册系列答案
相关题目