题目内容
如图1-2-9,测量人员沿直线MNP的方向测量,测得AB的仰角分别是∠AMB=30°,∠ANB=45°,∠APB=60°,且MN=PN=500 m,求塔高AB.
图1-2-9
解:设AB=h,
∵AB⊥MB,AB⊥NB,AB⊥PB,
又∠AMB=30°,∠ANB=45°,∠APB=60°,
∴MB=![]() h,NB=h,PB=
h,NB=h,PB=![]() h.
h.
在△MPB中,cos∠PMB=
 ,
,
在△MNB中,cos∠PMB=
![]() .
.
∴ ,
,
整理,得h=![]() (m).
(m).
∴塔高AB为![]() m.
m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在自然条件下,一年中10次测量的某种细菌一天内存活时间的统计表(时间近似到0.1小时)如下表所示:
| 日期 | 1月 1日 | 2月 28日 | 3月 21日 | 4月 27日 | 5月 27日 | 6月 21日 | 8月 13日 | 9月 20日 | 10月 25日 | 12月 21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 263 | 298 | 355 |
| 存活时间y(小时) | 5.6 | 10.2 | 12.3 | 16.4 | 17.3 | 19.4 | 16.4 | 12.5 | 8.5 | 5.4 |
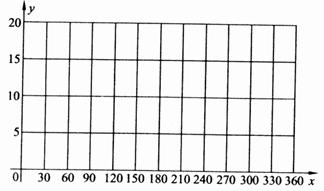
(1) 以日期在365天中的位置序号为横坐标,一天内存活时间为纵坐标,在给定坐标系中画出这些数据的散点图.
(2) 试选用一个形如![]() +t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
+t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
(3) 用(2)中的函数模型估计该种细菌一年中大约有多少天的存活时间大于15.9小时.