题目内容
 已知正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,则异面直线B1M与BC1所成角的大小为
已知正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,则异面直线B1M与BC1所成角的大小为
- A.

- B.
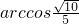
- C.
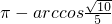
- D.
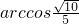
B
分析:取C1D1的中点N连接MN,B1N,∠NMB1即为异面直线B1M与BC1所成角,据已知中正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,解三角形NMB1即可得到异面直线B1M与BC1所成角的大小
解答:取N为C1D1的中点,连接MN,B1N
∵正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,
则∠NMB1即为异面直线B1M与BC1所成角
则MN=2 ,MB1=NB1=
,MB1=NB1= ,
,
则cos∠NMB1=
故异面直线B1M与BC1所成角的大小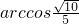
故选B
点评:本题考查的知识点是异面直线及其所成的角,其中通过平移法,构造出异面直线所成角的平面角是解答本题的关键.
分析:取C1D1的中点N连接MN,B1N,∠NMB1即为异面直线B1M与BC1所成角,据已知中正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,解三角形NMB1即可得到异面直线B1M与BC1所成角的大小
解答:取N为C1D1的中点,连接MN,B1N
∵正方体ABCD-A1B1C1D1的侧棱长为2,M为AB的中点,
则∠NMB1即为异面直线B1M与BC1所成角
则MN=2
 ,MB1=NB1=
,MB1=NB1= ,
,则cos∠NMB1=

故异面直线B1M与BC1所成角的大小
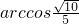
故选B
点评:本题考查的知识点是异面直线及其所成的角,其中通过平移法,构造出异面直线所成角的平面角是解答本题的关键.

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.