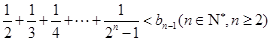题目内容
在数列![]() 中,
中,![]() ,其中
,其中![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)证明:存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立。
均成立。
解法一:(1)![]()
![]()
![]()
由此可猜想出数列![]() 的通项公式为
的通项公式为![]()
以下用数学归纳法证明:
①当![]() 时,
时,![]() ,等式成立.
,等式成立.
②假设当![]() 时等式成立,即
时等式成立,即![]()
那么![]()
![]()
这就是说,当![]() 时等式也成立。
时等式也成立。
根据①和②可知,等式![]() 对任何
对任何![]() 都成立。
都成立。
解法二:由![]()
![]() ,可得
,可得![]()
所以![]() 为等差数列,其公差为1,首项
为等差数列,其公差为1,首项
为0,故![]() ,所以数列
,所以数列![]() 的通项
的通项
公式为![]()
![]() 。
。
(2)设![]() ①
①
![]() ②
②
当![]() 时,①式减去②式,得
时,①式减去②式,得
![]()
![]()
这时数列![]() 的前n项和为
的前n项和为
![]()
当![]() 时,
时,![]() 。这时数列
。这时数列![]() 的前
的前![]() 项和
项和
![]() 。
。
(3)通过分析,推测数列![]() 的第一项
的第一项![]() 最大,
最大,
下面证明:![]() ③
③
由![]() 知
知![]() ,
,
要使③式成立,只要![]() ,
,
因为![]()
![]()
所以③式成立。
因此,存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立。
均成立。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,其中
,其中 .
. 项和
项和 ;
; ,使得
,使得 对任意
对任意 均成立.
均成立. 中,
中, (其中
(其中 为数列
为数列 的前n项和).
的前n项和). 的通项公式
的通项公式 ;
; ,求数列
,求数列 的前n项和
的前n项和 ,
, 中,
中, ,其中
,其中 .
. 为等差数列;
为等差数列;
 中,
中,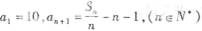 (其中
(其中 为数列
为数列 的前n项和).
的前n项和). 的通项公式
的通项公式 ;
; ,求数列
,求数列 的前n项和
的前n项和 ,
, 中,
中, ,其中
,其中 .
. 为等差数列;
为等差数列;