题目内容
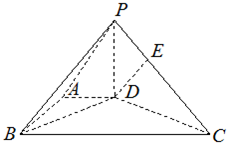 (2012•浙江模拟)如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,PD⊥平面ABCD,AD=1,AB=
(2012•浙江模拟)如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,PD⊥平面ABCD,AD=1,AB=| 3 |
(Ⅰ)求直线AB与平面PDC所成的角;
(Ⅱ)设点E在棱PC上,
| PE |
| PC |
分析:(Ⅰ)根据PD⊥平面ABCD,可得平面PDC⊥平面ABCD.过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G,则∠FDG为直线AB与平面PDC所成的角,从而可得结论;
(Ⅱ)连接EF,证明平面DEF∥平面PAB,从而EF∥AB,利用平行线的性质,可求λ的值.
(Ⅱ)连接EF,证明平面DEF∥平面PAB,从而EF∥AB,利用平行线的性质,可求λ的值.
解答: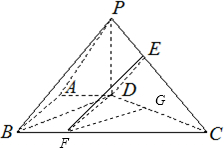 解:(Ⅰ)∵PD⊥平面ABCD,PD?平面ABCD.
解:(Ⅰ)∵PD⊥平面ABCD,PD?平面ABCD.
∴平面PDC⊥平面ABCD.
过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G,则∠FDG为直线AB与平面PDC所成的角.
在Rt△DFC中,∠DFC=90°,DF=
,CF=3,
∴tan∠FDG=
,∴∠FDG=60°.
即直线AB与平面PDC所成角为60°.…(6分)
(Ⅱ)连接EF,∵DF∥AB,∴DF∥平面PAB.
又∵DE∥平面PAB,DE∩DF=D
∴平面DEF∥平面PAB,
∵EF?平面DEF,∴EF∥AB.
又∵AD=1,BC=4,BF=1
∴
=
=
∴
=
,即λ=
…(14分)
 解:(Ⅰ)∵PD⊥平面ABCD,PD?平面ABCD.
解:(Ⅰ)∵PD⊥平面ABCD,PD?平面ABCD.∴平面PDC⊥平面ABCD.
过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G,则∠FDG为直线AB与平面PDC所成的角.
在Rt△DFC中,∠DFC=90°,DF=
| 3 |
∴tan∠FDG=
| 3 |
即直线AB与平面PDC所成角为60°.…(6分)
(Ⅱ)连接EF,∵DF∥AB,∴DF∥平面PAB.
又∵DE∥平面PAB,DE∩DF=D
∴平面DEF∥平面PAB,
∵EF?平面DEF,∴EF∥AB.
又∵AD=1,BC=4,BF=1
∴
| PE |
| PC |
| BF |
| BC |
| 1 |
| 4 |
∴
| PE |
| 1 |
| 4 |
| PC |
| 1 |
| 4 |
点评:本题通过分层设计,考查了空间平行、垂直,以及线面成角等知识,考查学生的空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 (2012•浙江模拟)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )
(2012•浙江模拟)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )