题目内容
如图所示,墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时不算,可重投,用随机模拟法求:
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?

解:记事件A={投中大圆内},
事件B={投中小圆与中圆形成的圆环},
事件C={投中大圆之外},
①用计算机产生两组[0,1]上的均匀随机数a1=RAND,b1=RAND;
②经过伸缩平移变换,a=16a1-8,b=16b1-8,得到两组[-8,8]的均匀随机数;
③统计投中大圆内的次数N1(即满足a2+b2<36的点(a,b)的个数),投中小圆与中圆形成的圆环的次数N2(即满足4<a2+b2<16的点(a,b)的个数),投中木板的总次数N(即满足-8<a<8,-8<b<8的点(a,b)的个数);
④计算频率fn(A)= ,即分别为概率P(A)、P(B)、P( C)的近似值。
,即分别为概率P(A)、P(B)、P( C)的近似值。
事件B={投中小圆与中圆形成的圆环},
事件C={投中大圆之外},
①用计算机产生两组[0,1]上的均匀随机数a1=RAND,b1=RAND;
②经过伸缩平移变换,a=16a1-8,b=16b1-8,得到两组[-8,8]的均匀随机数;
③统计投中大圆内的次数N1(即满足a2+b2<36的点(a,b)的个数),投中小圆与中圆形成的圆环的次数N2(即满足4<a2+b2<16的点(a,b)的个数),投中木板的总次数N(即满足-8<a<8,-8<b<8的点(a,b)的个数);
④计算频率fn(A)=
 ,即分别为概率P(A)、P(B)、P( C)的近似值。
,即分别为概率P(A)、P(B)、P( C)的近似值。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
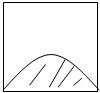 如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是
如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是 (2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为
(2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为
