题目内容
下列命题中,真命题是
- A.存在x∈R,
 +
+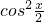 =
=
- B.任意x∈(0,π),sinx>cosx
- C.任意x∈(0,+∞),ex>1+x
- D.存在x∈R,x2+x=-1
C
分析:根据同角基本关系可知, +
+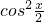 =1;例如x=
=1;例如x= ,但是sinx<cosx;令f(x)=ex-x-1,x>0,由导数可判断f(x)在x∈(0,+∞)单调递增,f(x)>f(0)=0,即ex>1+x;由于x2+x+1=
,但是sinx<cosx;令f(x)=ex-x-1,x>0,由导数可判断f(x)在x∈(0,+∞)单调递增,f(x)>f(0)=0,即ex>1+x;由于x2+x+1= 恒成立,
恒成立,
解答:根据同角基本关系可知, +
+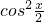 =1恒成立,故A错误
=1恒成立,故A错误
例如x= ,但是sinx<cosx,故B错误
,但是sinx<cosx,故B错误
令f(x)=ex-x-1,x>0,则f′(x)=ex-1>0,x∈(0,+∞)
∴f(x)在x∈(0,+∞)单调递增,
∴f(x)>f(0)=0,即ex>1+x,故C正确
由于x2+x+1= 恒成立,故x2+x=-1不可能成立,故D错误
恒成立,故x2+x=-1不可能成立,故D错误
故选C
点评:本题主要考查了命题真假的判断,解答的关键是熟练掌握基本知识并能灵活应用.
分析:根据同角基本关系可知,
 +
+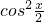 =1;例如x=
=1;例如x= ,但是sinx<cosx;令f(x)=ex-x-1,x>0,由导数可判断f(x)在x∈(0,+∞)单调递增,f(x)>f(0)=0,即ex>1+x;由于x2+x+1=
,但是sinx<cosx;令f(x)=ex-x-1,x>0,由导数可判断f(x)在x∈(0,+∞)单调递增,f(x)>f(0)=0,即ex>1+x;由于x2+x+1= 恒成立,
恒成立,解答:根据同角基本关系可知,
 +
+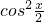 =1恒成立,故A错误
=1恒成立,故A错误例如x=
 ,但是sinx<cosx,故B错误
,但是sinx<cosx,故B错误令f(x)=ex-x-1,x>0,则f′(x)=ex-1>0,x∈(0,+∞)
∴f(x)在x∈(0,+∞)单调递增,
∴f(x)>f(0)=0,即ex>1+x,故C正确
由于x2+x+1=
 恒成立,故x2+x=-1不可能成立,故D错误
恒成立,故x2+x=-1不可能成立,故D错误故选C
点评:本题主要考查了命题真假的判断,解答的关键是熟练掌握基本知识并能灵活应用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
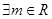 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1