题目内容
如图,平行六面体 中,侧棱
中,侧棱 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,
 点E在棱
点E在棱 上,则
上,则 的最小值为( )
的最小值为( )
A. | B.5 | C. | D.7 |
A
解析试题分析:
解:将面C1CB1B,B1BAA1打开,如图,由已知得C,B,A共线,连接AC1,则AC1为AE+C1E的最小值,
平行六面体中,侧棱B1B长为3,底面是边长为1的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,
∴CA=1+1=2,C1C=3,∴cos∠C1CA=cos60°= 解得C1A=
解得C1A= ,故AE+C1E的最小值为
,故AE+C1E的最小值为 ,故选A.
,故选A.
考点:线段和最小值
点评:本题考查线段和最小值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
已知 、
、 是不同的平面,
是不同的平面, 、
、 是不同的直线,则下列命题不正确的( )
是不同的直线,则下列命题不正确的( )
A.若 ∥ ∥ 则 则 | B.若 ∥ ∥ 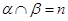 ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , , ,则 ,则 | D.若  则 则 ∥ ∥ |
对于两条不相交的空间直线 和
和 ,必定存在平面
,必定存在平面 ,使得 ( )
,使得 ( )
A. | B. | C. | D. |
设 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( )
A.若 ,则 ,则 |
B.若 ∥ ∥ ,则 ,则 |
C.若 ∥ ∥ , , , 则 , 则 ∥ ∥ |
D.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
已知m,n是两条不重合的直线, 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若m
 ,m
,m
 ,则
,则 ∥
∥ ; ②若
; ②若

 ,
,

 则
则 ∥
∥
③若m// ,n //
,n // ,m//n 则
,m//n 则 //
// ④若m
④若m
 ,m//
,m// ,则
,则


其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
已知三个平面 ,若
,若 ,且
,且 相交但不垂直,
相交但不垂直, 分别为
分别为 内的直线,则( )
内的直线,则( )
A. | B. | C. | D. |
设 为两条直线,
为两条直线, 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若 与 与 所成的角相等,则 所成的角相等,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.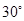 | B.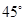 | C. | D. |
 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=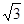 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 

