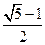题目内容
已知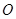 为原点,从椭圆 + =1的左焦点
为原点,从椭圆 + =1的左焦点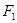 引圆
引圆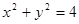 的切线
的切线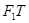 交椭圆于点
交椭圆于点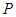 ,切点
,切点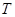 位于
位于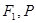 之间,
之间,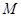 为线段
为线段 的中点,则
的中点,则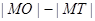 的值为_______________。
的值为_______________。
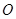 为原点,从椭圆 + =1的左焦点
为原点,从椭圆 + =1的左焦点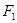 引圆
引圆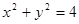 的切线
的切线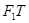 交椭圆于点
交椭圆于点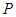 ,切点
,切点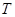 位于
位于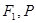 之间,
之间,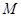 为线段
为线段 的中点,则
的中点,则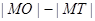 的值为_______________。
的值为_______________。
分析:利用三角形的中位线,可得|OM|=
 |PF′|,利用|MT|=|FT|-|FM|,可表示|MT|,再利用椭圆的定义,即可求得结论.
|PF′|,利用|MT|=|FT|-|FM|,可表示|MT|,再利用椭圆的定义,即可求得结论.解:由题意,设椭圆的右焦点为F′,连接PF′,OM,则|OM|=
 |PF′|
|PF′|∵|MT|=|FT|-|FM|=
 -
- |PF|="2"
|PF|="2"  -
- |PF|
|PF|∴|MO|-|MT|=
 |PF′|- 2
|PF′|- 2 +
+ |PF|=10-2
|PF|=10-2
故答案为:10-2


练习册系列答案
相关题目
 ,
,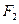 分别为椭圆
分别为椭圆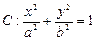
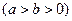 的左、右焦点,过
的左、右焦点,过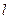 与椭圆
与椭圆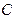 相交于
相交于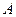 ,
,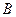 两点,直线
两点,直线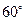 ,
,
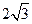 ;
;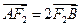 ,求椭圆
,求椭圆 中,
中, ,
, ,
, ,则
,则 ( )
( )



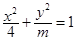 的离心率
的离心率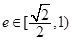 ,则
,则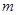 的取值范围为_____________.
的取值范围为_____________. 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线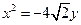 的焦点是椭圆
的焦点是椭圆
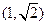 在椭圆
在椭圆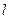 的方向向量为
的方向向量为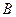 、
、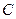 两点,求
两点,求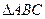 面积的最大值.
面积的最大值.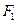 、
、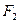 分别是椭圆
分别是椭圆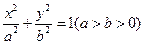 的左、右焦点,点B是其上顶点,椭圆的右准线与
的左、右焦点,点B是其上顶点,椭圆的右准线与
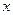 轴交于点N,且
轴交于点N,且 。
。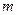 :
: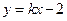 与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求
与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求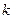 的值。
的值。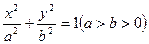 的左、右焦点分别为
的左、右焦点分别为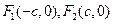 ,若椭圆上存在一点
,若椭圆上存在一点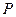 (非顶点)使
(非顶点)使
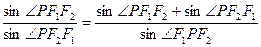 ,则该椭圆的离心率的取值范围是 .
,则该椭圆的离心率的取值范围是 .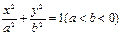 上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。
上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。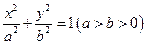 的四个顶点为A、B、C、D,若四边形ABCD的内切圆恰好过焦点,则椭圆的离心率为( )
的四个顶点为A、B、C、D,若四边形ABCD的内切圆恰好过焦点,则椭圆的离心率为( )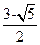 B.
B.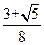 C.
C.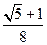 D.
D.