题目内容
已知函数f(x)=ax2-(a+1)x+1,
(Ⅰ)当x∈(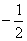 ,1)时,不等式f(x)>0恒成立,求实数a的取值范围;
,1)时,不等式f(x)>0恒成立,求实数a的取值范围;
(Ⅱ)设H(x)=[f(x)+a-1]ex,当a>-1且a≠0时,时求函数H(x)的单调区间和极值。
(Ⅰ)当x∈(
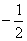 ,1)时,不等式f(x)>0恒成立,求实数a的取值范围;
,1)时,不等式f(x)>0恒成立,求实数a的取值范围;(Ⅱ)设H(x)=[f(x)+a-1]ex,当a>-1且a≠0时,时求函数H(x)的单调区间和极值。
解:(Ⅰ)①当a=0时,f(x)=-x+1在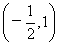 上f(x)>0一定成立;
上f(x)>0一定成立;
②当a≠0时,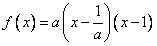 ,
,
当a>0时,二次函数y=f(x)的图象开口向上,且与x轴有两个交点(1,0)和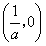 ,
,
要使f(x)>0在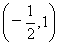 上恒成立,当且仅当
上恒成立,当且仅当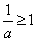 ,即0<a≤1;
,即0<a≤1;
当a<0时,二次函数y=f(x)的图象开口向下,且与x轴有两个交点(1,0)和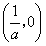 ,
,
要使f(x)>0在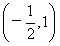 上恒成立,当且仅当
上恒成立,当且仅当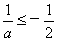 ,即-2≤a≤1;
,即-2≤a≤1;
综合可得实数a的取值范围是:-2≤a≤1;
(Ⅱ)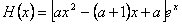 ,
,
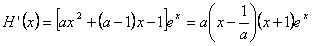 ,
,
令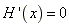 ,解得
,解得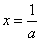 或x=-1,
或x=-1,
①当a>0时,则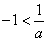 ,当x变化时,
,当x变化时,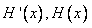 的变化情况如下表:
的变化情况如下表:
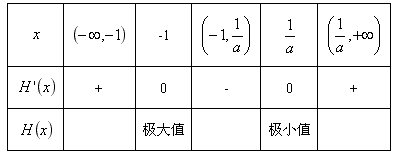
所以函数H(x)在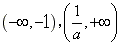 内是增函数,在
内是增函数,在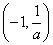 内是减函数,
内是减函数,
函数H(x)在x=-1处取得极大值H(-1),且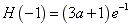 ;
;
函数H(x)在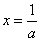 处取得极小值
处取得极小值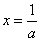 ,且
,且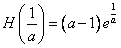 ;
;
②当-1<a<0时,则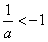 ,当x变化时,
,当x变化时,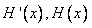 的变化情况如下表:
的变化情况如下表:
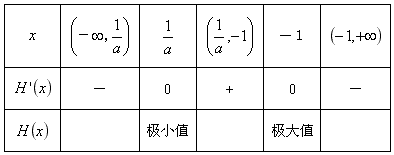
所以函数H(x)在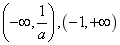 内是减函数,在
内是减函数,在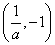 内是增函数,
内是增函数,
函数H(x)在x=-1处取得极大值H(-1),且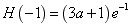 ;
;
函数H(x)在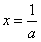 处取得极小值
处取得极小值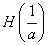 ,且
,且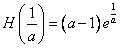 。
。
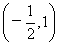 上f(x)>0一定成立;
上f(x)>0一定成立;②当a≠0时,
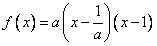 ,
,当a>0时,二次函数y=f(x)的图象开口向上,且与x轴有两个交点(1,0)和
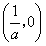 ,
,要使f(x)>0在
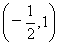 上恒成立,当且仅当
上恒成立,当且仅当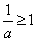 ,即0<a≤1;
,即0<a≤1;当a<0时,二次函数y=f(x)的图象开口向下,且与x轴有两个交点(1,0)和
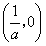 ,
,要使f(x)>0在
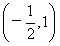 上恒成立,当且仅当
上恒成立,当且仅当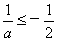 ,即-2≤a≤1;
,即-2≤a≤1;综合可得实数a的取值范围是:-2≤a≤1;
(Ⅱ)
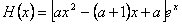 ,
,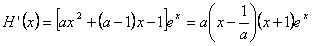 ,
,令
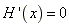 ,解得
,解得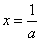 或x=-1,
或x=-1,①当a>0时,则
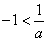 ,当x变化时,
,当x变化时,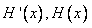 的变化情况如下表:
的变化情况如下表: 
所以函数H(x)在
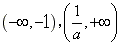 内是增函数,在
内是增函数,在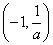 内是减函数,
内是减函数,函数H(x)在x=-1处取得极大值H(-1),且
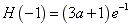 ;
;函数H(x)在
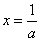 处取得极小值
处取得极小值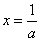 ,且
,且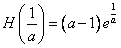 ;
;②当-1<a<0时,则
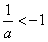 ,当x变化时,
,当x变化时,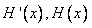 的变化情况如下表:
的变化情况如下表: 
所以函数H(x)在
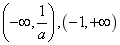 内是减函数,在
内是减函数,在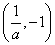 内是增函数,
内是增函数,函数H(x)在x=-1处取得极大值H(-1),且
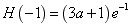 ;
;函数H(x)在
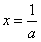 处取得极小值
处取得极小值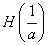 ,且
,且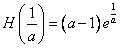 。
。 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |