题目内容
已知函数f(x)=2sin(2x+
),x∈R.
(1)画出函数f(x)在[0,π]上的图象;
(2)求函数f(x)的最小正周期;
(3)求函数f(x)的单调增区间.
| π | 3 |
(1)画出函数f(x)在[0,π]上的图象;
(2)求函数f(x)的最小正周期;
(3)求函数f(x)的单调增区间.
分析:(1)根据用五点法作函数y=Asin(ωx+∅)的图象的步骤和方法,做出函数f(x)在[0,π]上的图象.
(2)函数f(x)=Asin(ωx+∅)的最小正周期T=
求出结果.
(3)由2kπ-
≤2x+
≤2kπ+
,k∈z,解得x的范围,即得函数的单调增区间.
(2)函数f(x)=Asin(ωx+∅)的最小正周期T=
| 2π |
| ω |
(3)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:解:(1)列表:
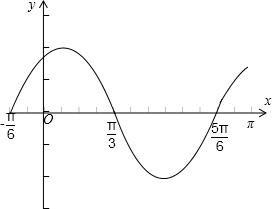
做出函数在一个周期上的简图,再根据图象的周期性特征,得到在一个周期[0,π]上的图象.
(2)函数f(x)的最小正周期T=
=π.
(3)由2kπ-
≤2x+
≤2kπ+
,k∈z,解得 kπ-
π ≤ x ≤kπ+
π,k∈z,
可得函数的增区间为[kπ-
π,kπ+
π],k∈Z.
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |

做出函数在一个周期上的简图,再根据图象的周期性特征,得到在一个周期[0,π]上的图象.
(2)函数f(x)的最小正周期T=
| 2π |
| 2 |
(3)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5 |
| 12 |
| 1 |
| 12 |
可得函数的增区间为[kπ-
| 5 |
| 12 |
| 1 |
| 12 |
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)的图象,以及函数y=Asin(ωx+∅)的单调性和周期性,属于中档题.

练习册系列答案
相关题目