题目内容
求下列各曲线的标准方程
(1)长轴长为12,离心率为
,焦点在x轴上的椭圆;
(2)双曲线 c1:9x2-16y2=576,双曲线c2与c1有共同的渐近线若c2过点(1,2)求c2的标准方程.
(1)长轴长为12,离心率为
| 2 | 3 |
(2)双曲线 c1:9x2-16y2=576,双曲线c2与c1有共同的渐近线若c2过点(1,2)求c2的标准方程.
分析:(1)由题意可知,2a=12,
=
,a2=b2+c2,解方程可求a,b进而可求椭圆方程
(2)由已知可设c2的方程9x2-16y2=λ,把点(1,2)代入双曲线方程可求λ,即可求解
| c |
| a |
| 2 |
| 3 |
(2)由已知可设c2的方程9x2-16y2=λ,把点(1,2)代入双曲线方程可求λ,即可求解
解答:解:(1)由题意可知,2a=12,
=
∵a2=b2+c2
∴a=6,b2=20
∴椭圆的方程为
+
=1
(2)双曲线c2与双曲线 c1:9x2-16y2=576有共同的渐近线
∴可设c2的方程9x2-16y2=λ
∵c2过点(1,2)
∴9×1-16×4=λ
∴λ=-55
∴所求的双曲线方程为9x2-16y2=-55
| c |
| a |
| 2 |
| 3 |
∵a2=b2+c2
∴a=6,b2=20
∴椭圆的方程为
| x2 |
| 36 |
| y2 |
| 20 |
(2)双曲线c2与双曲线 c1:9x2-16y2=576有共同的渐近线
∴可设c2的方程9x2-16y2=λ
∵c2过点(1,2)
∴9×1-16×4=λ
∴λ=-55
∴所求的双曲线方程为9x2-16y2=-55
点评:本题主要考查了由椭圆的性质求解椭圆方程,双曲线的性质的简单应用.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
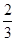 ,焦点在x轴上的椭圆;
,焦点在x轴上的椭圆;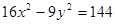 的左顶点.
的左顶点.