题目内容
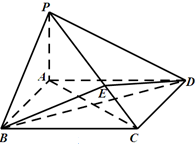
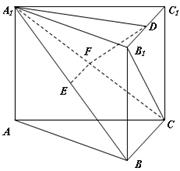
(本小题满分12分)右图是一个直三棱柱(以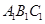 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为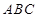 已知
已知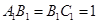 ,
,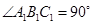 ,
,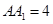 ,
,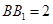 ,
,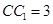

(Ⅰ)设点 是
是 的中点,证明:
的中点,证明: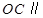 平面
平面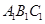 ;
;
(Ⅱ)求二面角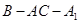 的大小;
的大小;
(Ⅰ)证明见解析(Ⅱ)
解析试题分析:(Ⅰ)证明:作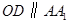 交
交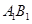 于
于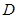 ,连
,连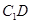 .
.
则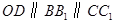 .
.
因为 是
是 的中点,
的中点,
所以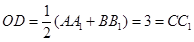
则四边形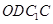 是平行四边形,
是平行四边形,
因此有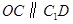
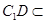 平面
平面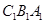
且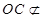 平面
平面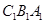 ,
,
则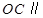 平面
平面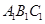 . ……6分
. ……6分
(Ⅱ)如图,以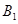 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
则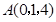 ,
,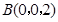 ,
,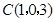 ,
, 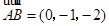 ,
,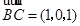 ,
,
设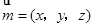 是平面
是平面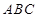 的一个法向量,则
的一个法向量,则
则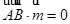 ,
,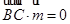 得:
得: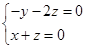
取 ,
,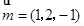
显然,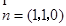 为平面
为平面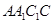 的一个法向量
的一个法向量
则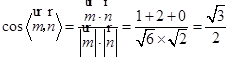 ,结合图形可知所求二面角为锐角,
,结合图形可知所求二面角为锐角,
所以二面角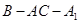 的大小是
的大小是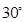 . ……12分
. ……12分
考点:本小题主要考查线面平行的证明和二面角的求法,考查学生的空间想象能力和运算求解能力.
点评:证明点评:遇到立体几何的证明题,要紧扣定理,要把定理要求的条件一一列清楚;而利用空间向量解决立体几何问题时,要建立右手空间直角坐标系,要准确计算.求二面角时,要注意二面角是锐角还是钝角.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。

 中,底面
中,底面 为矩形,
为矩形, 平面
平面 在线段
在线段 上,
上, 平面
平面 .
.
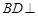 平面
平面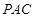 ;
;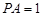 ,
,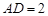 ,求二面角
,求二面角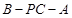 的正切值.
的正切值. 分别是
分别是 中点)
中点)
 平面
平面 ;
; 的体积.
的体积.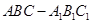 中,
中,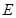 、
、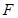 分别是
分别是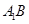 、
、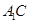 的中点,点
的中点,点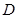 在
在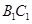 上,
上,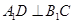 。
。
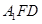
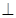 平面
平面

 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值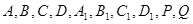 ;(2分)
;(2分)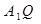 、
、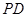 所成角为
所成角为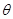 ,求
,求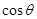 .(6分)
.(6分)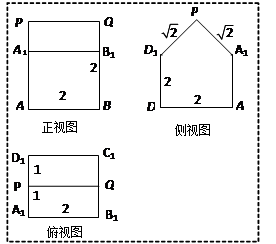


 A1D;
A1D; 。
。