题目内容
设全集U=R,A={x∈R|a≤x≤2},B={x∈R|2x+1≤x+3,且3x≥2}.
(1)若a=1,求A∪B,(?UA)∩B;
(2)若B⊆A,求实数a的取值范围.
(1)若a=1,求A∪B,(?UA)∩B;
(2)若B⊆A,求实数a的取值范围.
分析:(1)把a的值代入集合后直接利用集合的运算求解;
(2)根据子集的概念,利用集合端点值间的关系求解a的范围.
(2)根据子集的概念,利用集合端点值间的关系求解a的范围.
解答:解:(1)若a=1,则A={x|1≤x≤2},B={x|x≤2,且x≥
}={x|
≤x≤2},
此时A∪B={x|1≤x≤2}∪{x|
≤x≤2}={x|
≤x≤2}.

由?UA={x|x<1,或x>2},
∴(?UA)∩B={x|x<1,或x>2}∩{x|
≤x≤2}={x|
≤x<1};
(2)B={x|x≤2,且x≥
}={x|
≤x≤2},A={x∈R|a≤x≤2},
又∵B⊆A,
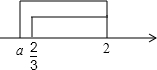
∴a≤
,
即实数a的取值范围是:a≤
.
| 2 |
| 3 |
| 2 |
| 3 |
此时A∪B={x|1≤x≤2}∪{x|
| 2 |
| 3 |
| 2 |
| 3 |

由?UA={x|x<1,或x>2},
∴(?UA)∩B={x|x<1,或x>2}∩{x|
| 2 |
| 3 |
| 2 |
| 3 |
(2)B={x|x≤2,且x≥
| 2 |
| 3 |
| 2 |
| 3 |
又∵B⊆A,

∴a≤
| 2 |
| 3 |
即实数a的取值范围是:a≤
| 2 |
| 3 |
点评:本题考查了交、并、补集的混合运算,考查了集合间的包含关系及运用,解答的关键是对端点值的取舍,是基础题.

练习册系列答案
相关题目
设全集U=R,A={x|ax+1=0},B={1,2},若A∩(?UB)=?,则实数a的取值集合是( )
| A、{0} | ||
| B、? | ||
C、{-1,-
| ||
D、{-1,-
|