Question

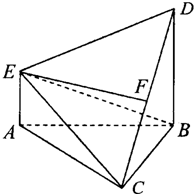如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，AE=1，CD与平面ABDE所成角的正弦值为

6

4

．
（1）若F是线段CD的中点，证明：EF⊥面DBC；
（2）求二面角D-EC-B的平面角的余弦值．

Answer 1

分析：（1）取AB的中点O，连结OC，OD，则OC⊥面ABD，∠CDO即是CD与平面ABDE所成角．求出BD=2．以O为原点，建立空间直角坐标系．取BC的中点为G，则AG⊥面BCD，利用

EF

∥

AG

，证明EF⊥面DBC．
（2）求出平面DEC的一个法向量和平面BCE的一个法向量．利用两个法向量的夹角求二面角D-EC-B的平面角

解答：解：（1）证明：取AB的中点O，连结OC，OD．
∵DB⊥平面ABC，DB?面ABD，根据直线和平面垂直的判定定理得，面ABD⊥平面ABC．
取AB的中点O，连结OC，OD．
∵△ABC是等边三角形，∴OC⊥AB，
根据平面和平面垂直的性质定理得则OC⊥面ABD，
∴OD是CD在平面ABDE上的射影，
∴∠CDO即是CD与平面ABDE所成角．
∴sin∠CDO=

OC

CD

=

6

4

，而OC=

3

，
∴CD=2

2

，∴BD=2．
取ED的中点为M，以O为原点，OC为x轴，OB为y轴，OM为z轴建立如图空间直角坐标系，则A（0，-1，0），C(

3

，0，0)，B(0，1，0)，D(0，1，2)，E(0，-1，1)，F(

3

2

，

1

2

，1)，
取BC的中点为G，则G（

3

2

，

1

2

，0），则AG⊥面BCD，因为

EF

=(

3

2

，

3

2

，0)，

AG

=(

3

2

，

3

2

，0)，
所以

EF

∥

AG

，所以EF⊥面DBC．
（2）解：由上面知：BF⊥面DEC，
又

BF

=(

3

2

，-

1

2

，1)，
取平面DEC的一个法向量

n

=(

3

，-1，2)
设平面BCE的一个法向量

m

=(x，y，z)，则

CE • m =0 CB • m =0

又

CE

=(-

3

，-1，1)，

CB

=(-

3

，1，0)，
所以

- 3 x-y+z=0 - 3 x+y=0

，令x=1，则y=

3

，z=2

3

．
由此得平面BCE的一个法向量

m

=(1，

3

，2

3

)．
则cos＜

m

，

n

＞=

m • n

| m || n |

=

4 3

4×2 2

=

6

4

，所以二面角D-EC-B的平面角的余弦值为

6

4

．

点评：本题考查空间直线、平面位置关系的判断，二面角大小求解，考查空间想象能力、推理论证、计算、转化能力．利用向量这一工具，解决空间几何体问题，能够降低思维难度．