题目内容
方程|lnx|=4sinx的解的个数是
6
6
．分析：分别画出y=4sinx的图象与y=lnx的图象，结合图象以及函数的单调性判定出交点的个数即可．
解答：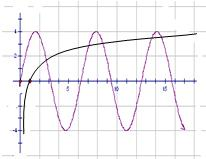
解：∵函数y=lnx，y=4sinx的图象如右图所示
由图象在[0，2π]内有1个交点，
在（2π，4π]内有2个交点，
在（4π，5π]内有2个交点，又5π＜16＜6π，
后面y=lnx的图象均在y=4sinx图象的上方．
故方程4sinx=lnx的根的个数为5个
又由y=|lnx|，可知方程|lnx|=4sinx的解的个数是6个．
故答案为6
解：∵函数y=lnx，y=4sinx的图象如右图所示由图象在[0，2π]内有1个交点，
在（2π，4π]内有2个交点，
在（4π，5π]内有2个交点，又5π＜16＜6π，
后面y=lnx的图象均在y=4sinx图象的上方．
故方程4sinx=lnx的根的个数为5个
又由y=|lnx|，可知方程|lnx|=4sinx的解的个数是6个．
故答案为6
点评：本题的考点是函数的零点与方程根的关系，主要考查用函数的思想研究方程问题，关键是合理构造函数，充分利用函数的图象，体现了数形结合的思想．属中档题．
练习册系列答案
相关题目