题目内容
13.将一个四面体PABC铁皮盒沿侧棱PA,PB,PC剪开,展平后恰好成一个正三角形.(Ⅰ)在四面体PABC中,求证:PA⊥BC.
(Ⅱ)若$PA=\sqrt{2}$,求铁皮盒的容积.
分析 (Ⅰ)四面体PABC为正四面体,取BC的中点O,连接PO,AO,则PO⊥BC,AO⊥BC,可得BC⊥平面PAO,即可证明PA⊥BC.
(Ⅱ)$PA=\sqrt{2}$,则四面体PABC的底面积为$\frac{\sqrt{3}}{4}×2$=$\frac{\sqrt{3}}{2}$,高为$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{6}}{3})^{2}}$=$\frac{2\sqrt{3}}{3}$,利用体积公式,即可求铁皮盒的容积.
解答 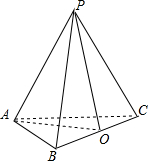 (Ⅰ)证明:∵将一个四面体PABC铁皮盒沿侧棱PA,PB,PC剪开,展平后恰好成一个正三角形,
(Ⅰ)证明:∵将一个四面体PABC铁皮盒沿侧棱PA,PB,PC剪开,展平后恰好成一个正三角形,
∴四面体PABC为正四面体,
取BC的中点O,连接PO,AO,则PO⊥BC,AO⊥BC,
又∵PO∩AO=O,
∴BC⊥平面PAO,
∵PA?平面PAO,
∴PA⊥BC.
(Ⅱ)解:$PA=\sqrt{2}$,则四面体PABC的底面积为$\frac{\sqrt{3}}{4}×2$=$\frac{\sqrt{3}}{2}$,高为$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{6}}{3})^{2}}$=$\frac{2\sqrt{3}}{3}$,
∴铁皮盒的容积为$\frac{1}{3}×\frac{\sqrt{3}}{2}×\frac{2\sqrt{3}}{3}$=$\frac{1}{3}$.
点评 本题考查线面垂直的判定与性质,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.把函数y=sinx-$\sqrt{3}$cosx的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的值可以是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
2.设a,b,c,x,y,z是正数,且a2+b2+c2=1,x2+y2+z2=4,ax+by+cz=2,则$\frac{a+b+c}{x+y+z}$( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |