题目内容
已知各项均为正数的数列{an}中,a1=1,Sn是数列an的前n项和,对任意的n∈N*,有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记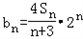 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记
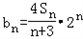 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.解:(1)∵a1=1,对任意的n∈N*,有2Sn=2pan2+pan﹣p
∴2a1=2pa12+pa1﹣p,
即2=2p+p﹣p,解得p=1;
(2)2Sn=2an2+an﹣1,①
2S n﹣1=2an﹣1 2+an﹣1﹣1,(n≥2),②
①﹣②即得(an﹣an﹣1﹣ )(an+an﹣1)=0,
)(an+an﹣1)=0,
因为an+an﹣1≠0,所以an﹣a n﹣1﹣ =0,
=0,
∴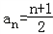
(3)2Sn=2an2+an﹣1=2×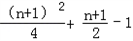 ,
,
∴Sn=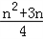 ,
,
∴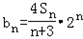 =n
=n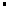 2n
2n
Tn=1×21+2×22+…+n×2n③
又2Tn=1×22+2×23+…+(n﹣1)×2n+n×2 n+1 ④
由④﹣③得,Tn=﹣1×21﹣(22+23+…+2n)+n2 n+1=(n﹣1)2 n+1+2
∴Tn=(n﹣1)2 n+1+2
∴2a1=2pa12+pa1﹣p,
即2=2p+p﹣p,解得p=1;
(2)2Sn=2an2+an﹣1,①
2S n﹣1=2an﹣1 2+an﹣1﹣1,(n≥2),②
①﹣②即得(an﹣an﹣1﹣
 )(an+an﹣1)=0,
)(an+an﹣1)=0,因为an+an﹣1≠0,所以an﹣a n﹣1﹣
 =0,
=0,∴
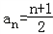
(3)2Sn=2an2+an﹣1=2×
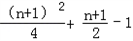 ,
,∴Sn=
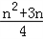 ,
,∴
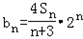 =n
=n 2n
2nTn=1×21+2×22+…+n×2n③
又2Tn=1×22+2×23+…+(n﹣1)×2n+n×2 n+1 ④
由④﹣③得,Tn=﹣1×21﹣(22+23+…+2n)+n2 n+1=(n﹣1)2 n+1+2
∴Tn=(n﹣1)2 n+1+2

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.