题目内容
正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为2a,求AC1与侧面ABB1A1所成的角.
分析:利用正三棱柱的性质,建立适当的空间直角坐标系,写出有关点的坐标.求角时有两种思路:一是由定义找出线面角,取A1B1的中点M,连结C1M,证明∠C1AM是AC1与面A1B所成的角;另一种是利用平面AB1的法向量n=(λ,x,y)求解.
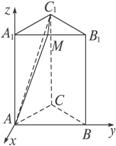
解:解法一:建立如图所示的空间直角坐标系,则A(0,0,0),B(0,a,0),A1(0,0, ![]() ),C1(-
),C1(-![]() a,
a, ![]() ,
,![]() a),取A1B1的中点M,则M(0,
a),取A1B1的中点M,则M(0,![]() ,
,![]() a),连结AM,MC1,有
a),连结AM,MC1,有
![]() =(-
=(-![]() a,0,0),
a,0,0),![]() =(0,a,0),
=(0,a,0),![]() =(0,0,
=(0,0,![]() a).
a).
由于![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
∴MC1⊥面ABB1A1.
∴∠C1AM是AC1与侧面A1B所成的角.
∵![]() =(-
=(-![]() a,
a,![]() ,
,![]() a),
a),![]() =(0,
=(0,![]() ,
,![]() a),
a),
∴![]() ·
·![]() =0+
=0+![]() +2a2=
+2a2=![]() .
.
而|![]() |=
|=![]() ,
,
|![]() |=
|=![]() ,
,
∴cos〈![]() ,
,![]() 〉=
〉=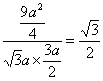 .
.
∴〈![]() ,
,![]() 〉=30°,即AC1与侧面AB1所成的角为30°.
〉=30°,即AC1与侧面AB1所成的角为30°.
解法二:(法向量法)(接方法一)![]() =(0,0,
=(0,0,![]() a).
a).
设侧面A1B的法向量n=(λ,x,y),
∴n·![]() =0且n·
=0且n·![]() =0.
=0.
∴ax=0,且![]() ay=0.
ay=0.
∴x=y=0.故n=(λ,0,0).
∵![]() =(-
=(-![]() a,
a,![]() ,
,![]() a),
a),
∴cos〈![]() ,n〉=
,n〉=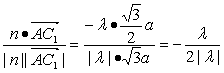 .
.
∴|cos〈![]() ,n〉|=
,n〉|=![]() ,∴〈
,∴〈![]() ,
,![]() 〉=30°,即AC1与侧面AB1所成的角为30°.
〉=30°,即AC1与侧面AB1所成的角为30°.
点拨:充分利用图形的几何特征建立适当的空间直角坐标系,再用向量的有关知识求解线面角.方法二给出了一般的方法,先求平面法向量与斜线夹角,再进行换算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.