题目内容
6．已知抛物线C：y2=4x，过x轴上的一定点Q（a，0）的直线l交抛物线C于A、B两点（a为大于零的正常数）．（1）设O为坐标原点，求△ABO面积的最小值；
（2）若点M为直线x=-a上任意一点，探求：直线MA，MQ，MB的斜率是否成等差数列？若是，则给出证明；若不是，则说明理由．
分析 （1）联立直线AB与抛物线方程，利用韦达定理可得结论；
（2）设M（-a，t），通过计算2kMQ与kMA+kMB的值即得结论．
解答 解：（1）设直线AB的方程为：my=x-a，
联立方程组$\left\{\begin{array}{l}{my=x-a}\\{{y}^{2}=4x}\end{array}\right.$，消去x可得：y2-4my-4a=0，
设A（x1，y1），B（x2，y2），则y1+y2=4m，y1y2=-4a，
∴S△AOB=$\frac{1}{2}$•a•|y1-y2|=2a$\sqrt{a+{m}^{2}}$，
所以当m=0时，S△AOB有最小值2a$\sqrt{a}$；
（2）结论：直线MA，MQ，MB的斜率成等差数列．
证明如下：
设M（-a，t），∴kMQ=$\frac{t}{-2a}$，
而kMA+kMB=$\frac{{y}_{1}-t}{{x}_{1}+a}$+$\frac{{y}_{2}-t}{{x}_{2}+a}$=$\frac{\frac{{y}_{1}{y}_{2}}{4}（{y}_{1}+{y}_{2}）+a（{y}_{1}+{y}_{2}）-t（{x}_{1}+{x}_{2}）-at}{{x}_{1}{x}_{2}+a（{x}_{1}+{x}_{2}）+{a}^{2}}$ （*）
因为x1x2=$\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}}{16}$=a2，x1+x2=m（y1+y2）+2a=4m2+2a，
代入（*）式，可得kMA+kMB=$\frac{-4t（a+{m}^{2}）}{4a（a+{m}^{2}）}$=-$\frac{t}{a}$，
∴kMA+kMB=2kMQ，
所以直线MA，MQ，MB的斜率成等差数列．
点评 本题是一道直线与圆锥曲线的综合题，考查运算求解能力，涉及到韦达定理、斜率的计算、等差中项的性质、三角形的面积计算公式等知识，注意解题方法的积累，属于中档题．
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案| A． | $\frac{25}{2}$ | B． | $\frac{\sqrt{10}}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$或$\frac{1}{16}$ | C． | $\frac{1}{16}$ | D． | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
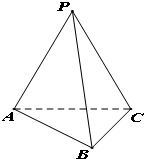如图，在三棱锥P-ABC中，平面APC⊥平面ABC，且PA=PB=PC=4，AB=BC=2．
的顶点都在抛物线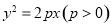
上，且
，
，则点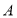
到抛物线的焦点的距离是______________．
如图，椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）左、右顶点为A，B，左、右焦点为F1，F2，|AB|=4，|F1F2|=2$\sqrt{3}$．直线y=kx+m（k＞0）交椭圆E于C，D两点，与线段F1F2、椭圆短轴分别交于M，N两点（M，N不重合），且|CM|=|DN|．