题目内容
若直线kx-y-4k=0与曲线y=
有公共的点,则实数k的取值范围( )
| 4-x2 |
分析:曲线y=
表示x2+y2=4(y≥0),即圆的上半圆,直线kx-y-4k=0恒过定点(4,0),利用点到直线的距离公式可得结论.
| 4-x2 |
解答: 解:曲线y=
解:曲线y=
表示x2+y2=4(y≥0),即圆的上半圆,直线kx-y-4k=0恒过定点(4,0)
当直线与x2+y2=4(y≥0)相切时,
=2,
∴k=-
∴直线kx-y-4k=0与曲线y=
有公共的点时,实数k的取值范围是[-
,0]
故选D.
 解:曲线y=
解:曲线y=| 4-x2 |
当直线与x2+y2=4(y≥0)相切时,
| |4k| | ||
|
∴k=-
| ||
| 3 |
∴直线kx-y-4k=0与曲线y=
| 4-x2 |
| ||
| 3 |
故选D.
点评:本题考查直线与圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
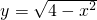 有公共的点,则实数k的取值范围
有公共的点,则实数k的取值范围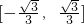



 有公共的点,则实数k的取值范围( )
有公共的点,则实数k的取值范围( )



 有公共的点,则实数k的取值范围( )
有公共的点,则实数k的取值范围( )


