题目内容
设各项均为正数的数列{an}满足a1=2,an=
an+2(n∈N*).(1)若a2=
,求a3,a4,并猜想a2 008的值(不需证明);
(2)记bn=a1a2…an(n∈N*),若bn≥2
对n≥2恒成立,求a2的值及数列{bn}的通项公式.
解:(1)因a1=2,a2=2-2,故a3==24,
a4==2-8.
由此有a1=,a2=
,a3=
,a4=
,故猜想{an}的通项为an=
(n∈N*).
从而a2 008=
.
(2)令xn=log2an,Sn表示xn的前n项和,则bn=
.
由题设知x1=1且xn=
xn+1+xn+2(n∈N*);①
Sn=x1+x2+…+xn≥
(n≥2).②
因②式对n=2成立,有
≤x1+x2,又x1=1得x2≥
.③
下用反证法证明:x2≤
.假设x2＞
.
由①得xn+2+2xn+1=(xn+2+
xn+1)+ 
xn+1=
(xn+1+2xn).
因此数列{xn+1+2xn}是首项为x2+2,公比为
的等比数列.
故xn+1+2xn=(x2+2)
(n∈N*).④
又由①知xn+2-
xn+1=(xn-
xn+1)-
xn+1=-2(xn+1-
xn),
因此{xn+1-
xn}是首项为x2-
,公比为-2的等比数列,所以xn+1-
xn=(x2-
)(-2)n-1(n∈N*).⑤
由④-⑤得
xn=(x2+2)
-(x2-
)(-2)n-1(n∈N*).⑥
对n求和得
Sn=(x2+2)(2-
)-(x2-
)
(n∈N*).⑦
由题设知S2k+1≥
,且由反证假设x2＞
有
(x2+2)(2
)-(x2-
)
≥
(k∈N*).
从而(x2-
)·
≤(x2+2)(2
)-
＜2x2+
(k∈N*),
即不等式22k+1＜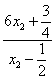
-1对k∈N*恒成立.但这是不可能的,矛盾.
因此x2≤
,结合③式知x2=
.因此a2=
=2.
将x2=
代入⑦式得Sn=2-
(n∈N*),
所以bn=
=
(n∈N*).
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目