题目内容
设x=
,y=2+
π,集合M={m|m=a+b
,a∈Q,b∈Q},那么x,y与集合M的关系是( )
| 1 | ||
3-5
|
| 2 |
| 2 |
分析:对元素x进行整理,分母有理化,分子和分母同乘以分母的有理化因式,得到结果,根据π不是有理数得到y不是集M的元素.
解答:解:x=
=
=-
-
∈M
∵π∉Q
∴y=2+
π∉M
故选B.
| 1 | ||
3-5
|
3+5
| ||||
(3-5
|
| 3 |
| 41 |
| 5 |
| 41 |
| 2 |
∵π∉Q
∴y=2+
| 2 |
故选B.
点评:本题考查元素与集合关系的判断,本题解题的关键是整理数字成集合中元素所对应的形式,属于基础题.

练习册系列答案
相关题目
设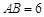 ,在线段
,在线段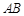 上任取两点C,D(端点
上任取两点C,D(端点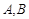 除外),将线段
除外),将线段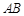 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
|
|
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 |
0.05 |
0.32 |
0.38 |
0.73 |
|
Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0.86 |
|
|
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 |
0.36 |
0.35 |
0.95 |
0.14 |
|
Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是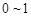 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是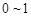 之间的均匀随机数)
之间的均匀随机数)