题目内容
若y=f(x)是奇函数,当x>0时,f(x)=2x+1,则 =
=
- A.7
- B.

- C.-4
- D.

C
分析:判断出 <0,再利用符号转化为大于零,再代入解析式根据“
<0,再利用符号转化为大于零,再代入解析式根据“ ”进行求解.
”进行求解.
解答:∵ =-
=- <0,且y=f(x)是奇函数,
<0,且y=f(x)是奇函数,
∴ =-f(
=-f( )
)
∵当x>0时,f(x)=2x+1,∴ =-(
=-( +1)=-4,
+1)=-4,
故选C.
点评:本题考查了偶函数的性质和对数运算性质,即根据偶函数对应的关系式,将所求的函数值进行转化,转化到已知范围内求解,考查了转化思想.
分析:判断出
 <0,再利用符号转化为大于零,再代入解析式根据“
<0,再利用符号转化为大于零,再代入解析式根据“ ”进行求解.
”进行求解.解答:∵
 =-
=- <0,且y=f(x)是奇函数,
<0,且y=f(x)是奇函数,∴
 =-f(
=-f( )
)∵当x>0时,f(x)=2x+1,∴
 =-(
=-( +1)=-4,
+1)=-4,故选C.
点评:本题考查了偶函数的性质和对数运算性质,即根据偶函数对应的关系式,将所求的函数值进行转化,转化到已知范围内求解,考查了转化思想.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
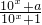 是奇函数.
是奇函数.