题目内容

已知函数f（x）=log_a（1-x）+log_a（x+3），若函数f（x）的最小值为-2，则实数a的值为________．

$\text{[math]}$
分析：先求函数的定义域，再利用对数运算性质将已知函数化简为二次函数与对数函数的复合，由于内层函数有最大值，故外层函数定位减函数，依题意列方程即可解得a值
解答：由 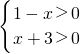$\text{[math]}$ 得函数f（x）的定义域为（-3，1）
f（x）=log_a（1-x）+log_a（x+3）=log_a[（1-x）（x+3）]，
∵y=（1-x）（x+3）=-（x+1）²+4在定义域（-3，1）上有最大值4，没有最小值
∴要使函数f（x）的最小值为-2，须a满足 $\text{[math]}$
解得a= $\text{[math]}$
故答案为 $\text{[math]}$
点评：本题考查了对数的定义和运算法则，对数函数的定义域及其单调性，复合函数的最值的求法，推理运算能力

练习册系列答案

一线名师云南密卷系列答案

化学教与学系列答案

四川新教材新中考系列答案

系统分类总复习系列答案

新课标阶梯阅读训练系列答案

考前模拟预测试卷系列答案

同步词汇训练系列答案

优加学案创新金卷系列答案

单元自测系列答案

冠亚中考模拟试题系列答案

相关题目

已知函数f（x）=2x-2+ae^-x（a∈R）
（1）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求a的值；
（2）当a=1时，若直线l：y=kx-2与曲线y=f（x）在（-∞，0）上有公共点，求k的取值范围．

已知函数f（x）=x²+2|lnx-1|．
（1）求函数y=f（x）的最小值；
（2）证明：对任意x∈[1，+∞），lnx≥

恒成立；
（3）对于函数f（x）图象上的不同两点A（x₁，y₁），B（x₂，y₂）（x₁＜x₂），如果在函数f（x）图象上存在点M（x₀，y₀）（其中x₀∈（x₁，x₂））使得点M处的切线l∥AB，则称直线AB存在“伴侣切线”．特别地，当x₀=

时，又称直线AB存在“中值伴侣切线”．试问：当x≥e时，对于函数f（x）图象上不同两点A、B，直线AB是否存在“中值伴侣切线”？证明你的结论．

已知函数f（x）=x²-bx的图象在点A（1，f（1））处的切线l与直线x+3y-1=0垂直，若数列{

}的前n项和为S_n，则S₂₀₁₂的值为（　　）

已知函数f（x）=xlnx
（Ⅰ）求函数f（x）的极值点；
（Ⅱ）若直线l过点（0，-1），并且与曲线y=f（x）相切，求直线l的方程．

已知函数f（x）=

，a≠0且a≠1．
（1）试就实数a的不同取值，写出该函数的单调增区间；
（2）已知当x＞0时，函数在（0，

）上单调递减，在（

，+∞）上单调递增，求a的值并写出函数的解析式；
（3）记（2）中的函数图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出直线l的方程；若不存在，请说明理由．