题目内容
下列说法错误的是
- A.若z∈C,则|z|=1的充要条件是
 =
=
- B.若z=sinθ+icosθ(其中0<θ<
 ),则(
),则( )2<0
)2<0 - C.若方程x2+bx+c=0的系数不都是实数,则此方程必有虚数根
- D.复数(a-b)+(a+b)i为纯虚数的充要条件是a、b∈R,且a=b
D
分析:对各个选项逐个加以判断:根据复数性质 ,说明A选项不错;根据复数运算法则进行推导,可由z=sinθ+
,说明A选项不错;根据复数运算法则进行推导,可由z=sinθ+
icosθ(其中0<θ< ),推出(
),推出( )2<0,说明B选项不错;根据复系数一元二次方程必定有虚数根据的定理,可知C选项也不错.A、B、C都不错,很容易就有找出D选项的反例,因此不难选出正确答案了.
)2<0,说明B选项不错;根据复系数一元二次方程必定有虚数根据的定理,可知C选项也不错.A、B、C都不错,很容易就有找出D选项的反例,因此不难选出正确答案了.
解答:对于A:根据复数的共轭的性质 ,得到|z|=1?
,得到|z|=1?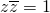 ?
? =
= ,故A正确;
,故A正确;
对于B,因为z=sinθ+icosθ,所以
得出:( )2=
)2=
∵0<θ< ,∴cosθ∈(0,1);∴(
,∴cosθ∈(0,1);∴( )2<0,故B正确;
)2<0,故B正确;
对于C:若方程x2+bx+c=0的系数不都是实数,根据复数相等的含义,不管哪一项系数为虚数,必定要有虚数根与这个系数相乘,才能使结果为零而不含虚数单位i,所以方程必定有虚数根即方程的两个根不可能都是实数,C也正确;
对于D:复数(a-b)+(a+b)i为纯虚数的充要条件是a、b∈R,且a=b,很明显是错误的,因为当a=b=0时,复数(a-b)+(a+b)i不是虚数,故D选项是错误的
故选D
点评:本题以复数为例,考查了充分条件与必要条件的判断,属于中档题.熟记复数的运算法则与运算性质,是解决好本题的关键所在.
分析:对各个选项逐个加以判断:根据复数性质
 ,说明A选项不错;根据复数运算法则进行推导,可由z=sinθ+
,说明A选项不错;根据复数运算法则进行推导,可由z=sinθ+icosθ(其中0<θ<
 ),推出(
),推出( )2<0,说明B选项不错;根据复系数一元二次方程必定有虚数根据的定理,可知C选项也不错.A、B、C都不错,很容易就有找出D选项的反例,因此不难选出正确答案了.
)2<0,说明B选项不错;根据复系数一元二次方程必定有虚数根据的定理,可知C选项也不错.A、B、C都不错,很容易就有找出D选项的反例,因此不难选出正确答案了.解答:对于A:根据复数的共轭的性质
 ,得到|z|=1?
,得到|z|=1?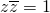 ?
? =
= ,故A正确;
,故A正确;对于B,因为z=sinθ+icosθ,所以

得出:(
 )2=
)2=
∵0<θ<
 ,∴cosθ∈(0,1);∴(
,∴cosθ∈(0,1);∴( )2<0,故B正确;
)2<0,故B正确;对于C:若方程x2+bx+c=0的系数不都是实数,根据复数相等的含义,不管哪一项系数为虚数,必定要有虚数根与这个系数相乘,才能使结果为零而不含虚数单位i,所以方程必定有虚数根即方程的两个根不可能都是实数,C也正确;
对于D:复数(a-b)+(a+b)i为纯虚数的充要条件是a、b∈R,且a=b,很明显是错误的,因为当a=b=0时,复数(a-b)+(a+b)i不是虚数,故D选项是错误的
故选D
点评:本题以复数为例,考查了充分条件与必要条件的判断,属于中档题.熟记复数的运算法则与运算性质,是解决好本题的关键所在.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知f:A→B是从集合A到B的映射,下列说法错误的是
A.A中的每一个元素在B中必有象
B.B中可能有元素在A中没有原象
C.A中两个不同的元素在B中的象一定不相同
D.B中的某个元素在A中的原象可能不只一个
下列说法错误的是 ( )
A.命题“若 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若 ,则 ,则 ”. ”. |
B.“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
C.若 且 且 为假命题,则 为假命题,则 、 、 均为假命题. 均为假命题. |
D.命题 :存在 :存在 使得 使得 . 则 . 则 :任意 :任意 ,均有 ,均有 . . |
 是
是 或
或 的充分不必要条件
的充分不必要条件
 ,则
,则

 的绝对值越接近
的绝对值越接近 ,表示两变量的相关性越强.
,表示两变量的相关性越强.