题目内容
(1)已知双曲线与椭圆
+
=1共焦点,它们的离心率之和为
,求双曲线方程.
(2)P为椭圆
+
=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,求△F1PF2的面积.
| x2 |
| 25 |
| y2 |
| 9 |
| 14 |
| 5 |
(2)P为椭圆
| x2 |
| 100 |
| y2 |
| 64 |
分析:(1)由题意可知双曲线的焦点在x轴,并求得焦点为F(±4,0),离心率为2,从而求出c,a,b得到双曲线方程;
(2)根据椭圆的定义,得PF1+PF2=2a…①,再在△F1PF2中用余弦定理,得PF12+PF22-PF1•PF2…②.由①②联解,得PF1•PF2,最后用根据正弦定理关于面积的公式,可得△PF1F2的面积.
(2)根据椭圆的定义,得PF1+PF2=2a…①,再在△F1PF2中用余弦定理,得PF12+PF22-PF1•PF2…②.由①②联解,得PF1•PF2,最后用根据正弦定理关于面积的公式,可得△PF1F2的面积.
解答:解:(1)∵椭圆焦点为F(±4,0),离心率为e=
,而双曲线与椭圆共焦点,
∴双曲线的焦点为F(±4,0),又它们的离心率之和为
,
设该双曲线的离心率为e,则e+
=
,
∴e=2,即
=2,而c=4,
∴a=2,b=2
.
∴双曲线方程为:
-
=1;
(2)∵椭圆方程是
+
=1,
∴a2=100,b2=64.可得a=10,c2=100-64=36,即c=6.
∵P是椭圆
+
=1上的一点,F1、F2是焦点,
∴根据椭圆的定义,得PF1+PF2=2a=20…①
又∵△F1PF2中,∠F1PF2=60°且F1F2=2c=12
∴根据余弦定理,得F1F22=PF12+PF22-2PF1•PF2cos60°=144,
即PF12+PF22-PF1•PF2=144…②
∴①②联解,得PF1•PF2=
∴△PF1F2的面积为:S=
PF1•PF2sin60°=
.
| 4 |
| 5 |
∴双曲线的焦点为F(±4,0),又它们的离心率之和为
| 14 |
| 5 |
设该双曲线的离心率为e,则e+
| 4 |
| 5 |
| 14 |
| 5 |
∴e=2,即
| c |
| a |
∴a=2,b=2
| 3 |
∴双曲线方程为:
| x2 |
| 4 |
| y2 |
| 12 |
(2)∵椭圆方程是
| x2 |
| 100 |
| y2 |
| 64 |
∴a2=100,b2=64.可得a=10,c2=100-64=36,即c=6.
∵P是椭圆
| x2 |
| 100 |
| y2 |
| 64 |
∴根据椭圆的定义,得PF1+PF2=2a=20…①
又∵△F1PF2中,∠F1PF2=60°且F1F2=2c=12
∴根据余弦定理,得F1F22=PF12+PF22-2PF1•PF2cos60°=144,
即PF12+PF22-PF1•PF2=144…②
∴①②联解,得PF1•PF2=
| 256 |
| 3 |
∴△PF1F2的面积为:S=
| 1 |
| 2 |
| 64 |
| 3 |
| 3 |
点评:本题考查椭圆、双曲线的标准方程与双曲线的简单性质,掌握椭圆、双曲线的方程与性质是解决问题的基础,也是关键,属于基础题.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: :
: 与双曲线
与双曲线 :
: 有相同的焦点
有相同的焦点 ,
, 是椭圆
是椭圆 的周长为
的周长为 ,求椭圆
,求椭圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 的距离为
的距离为 ,
, 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;
 :
: (
(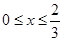 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧 :
: )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”.设过点
”.设过点 两点,
两点, ,
,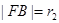 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.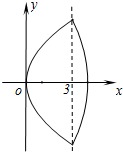 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: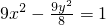 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;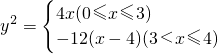 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 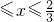 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: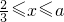 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.