题目内容
已知函数 图象在x=1处的切线方程为2y﹣1=0.
图象在x=1处的切线方程为2y﹣1=0.
 图象在x=1处的切线方程为2y﹣1=0.
图象在x=1处的切线方程为2y﹣1=0. (1) 求函数f(x)的极值;
(2)若△ABC的三个顶点(B在A、C之间)在曲线y=f(x)+ln(x﹣1)(x>1)上,试探究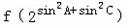 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(2)若△ABC的三个顶点(B在A、C之间)在曲线y=f(x)+ln(x﹣1)(x>1)上,试探究
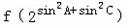 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.解:(1)求导得:f'(x)= ,
,
由题意得:f'(1)=0,f(1)= ,
,

 =0,
=0, =
= ,
,
解得a=1,b=0,
 由f'(x)=﹣
由f'(x)=﹣ >0,解得:x<﹣1或x>1;
>0,解得:x<﹣1或x>1;
由f'(x)=﹣ <0,解得:﹣1<x<1,
<0,解得:﹣1<x<1,
 f(x)在(﹣
f(x)在(﹣ ,﹣1)或(1,+
,﹣1)或(1,+ )上是减函数,在(﹣1,1)上是增函数,
)上是减函数,在(﹣1,1)上是增函数,
则f(x)的极小值为f(﹣1)=﹣ ,f(x)的极大值为f(1)=
,f(x)的极大值为f(1)= ;
;
(2) 设A(x1,y1)、B(x2,y2)、C(x3,y3),
且x1<x2<x3,y=f(x)+ln(x﹣1)= +ln(x﹣1)(x>1),
+ln(x﹣1)(x>1),
 y'=
y'= >0,
>0,
 函数在(1,+
函数在(1,+ )上单调递增,
)上单调递增,
由x1<x2<x3得:y1<y2<y3,

 ·
· =(x1﹣x2)(x3﹣x2)+(y1﹣y2)(y3﹣y2)<0,
=(x1﹣x2)(x3﹣x2)+(y1﹣y2)(y3﹣y2)<0,
 B是钝角,由余弦定理得cosB=
B是钝角,由余弦定理得cosB= <0,即a2+c2<b2,
<0,即a2+c2<b2,
由正弦定理得:sin2A+sin2C<sin2B,则 >
> >1,
>1,
又 f(x)是(1,+
f(x)是(1,+ )上的增函数,
)上的增函数,

 >
> .
.
 ,
, 由题意得:f'(1)=0,f(1)=
 ,
,
 =0,
=0, =
= ,
,解得a=1,b=0,
 由f'(x)=﹣
由f'(x)=﹣ >0,解得:x<﹣1或x>1;
>0,解得:x<﹣1或x>1;由f'(x)=﹣
 <0,解得:﹣1<x<1,
<0,解得:﹣1<x<1, f(x)在(﹣
f(x)在(﹣ ,﹣1)或(1,+
,﹣1)或(1,+ )上是减函数,在(﹣1,1)上是增函数,
)上是减函数,在(﹣1,1)上是增函数,则f(x)的极小值为f(﹣1)=﹣
 ,f(x)的极大值为f(1)=
,f(x)的极大值为f(1)= ;
;(2) 设A(x1,y1)、B(x2,y2)、C(x3,y3),
且x1<x2<x3,y=f(x)+ln(x﹣1)=
 +ln(x﹣1)(x>1),
+ln(x﹣1)(x>1), y'=
y'= >0,
>0, 函数在(1,+
函数在(1,+ )上单调递增,
)上单调递增, 由x1<x2<x3得:y1<y2<y3,

 ·
· =(x1﹣x2)(x3﹣x2)+(y1﹣y2)(y3﹣y2)<0,
=(x1﹣x2)(x3﹣x2)+(y1﹣y2)(y3﹣y2)<0, B是钝角,由余弦定理得cosB=
B是钝角,由余弦定理得cosB= <0,即a2+c2<b2,
<0,即a2+c2<b2,由正弦定理得:sin2A+sin2C<sin2B,则
 >
> >1,
>1,又
 f(x)是(1,+
f(x)是(1,+ )上的增函数,
)上的增函数,
 >
> .
.
练习册系列答案
相关题目
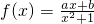 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0.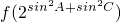 与
与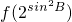 的大小关系,并说明理由.
的大小关系,并说明理由. 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由.
的大小关系,并说明理由. 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由;
的大小关系,并说明理由; (n∈N*).
(n∈N*).