题目内容
已知双曲线C：
-y2=1,以C的右焦点为圆心且与其渐近线相切的圆方程为___________，定点（3，0）与C上动点距离的最小值为____________．
(x-)2+y2=2，
解析：本题考查双曲线的几何性质以及轨迹方程的求法．已知双曲线方程为
-y2=1，所以右焦点坐标为F(
，0)，渐进线方程为了y=±
.所以以F为圆心与渐进线相切的圆的半径为点F到y=±
的距离，所以r=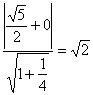
,所以圆的方程为：(x-
)2+y2=2．设(x，y)为双曲线右支上任意一点，则有x≥2，所以d2=(x-3)2+y2=(x-3)2+
-6x+8
=
S，由x≥2知x=
时d取得最小值，最小值是
．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
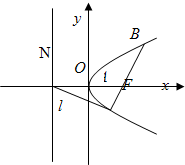已知双曲线C：y2-x2=8，直线l：y=-x+8，若椭圆M与双曲线C有公共焦点，与直线l有公共点P，求椭圆长轴的最小值及此时P点的坐标．
-y2=1,以C的右焦点为圆心且与其渐近线相切的圆方程为__________,若动点A，B分别在双曲线C的两条渐近线上，且
=2,则线段AB中点的轨迹方程为________.
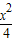-y2=1，P是C上的任意点．
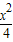-y2=1，P是C上的任意点．