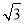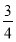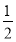题目内容
如图，在长方体ABCD－A1B1C1D1中，底面A1B1C1D1是正方形，O是BD的中点，E是棱AA1上任意一点．
(1)证明：BD⊥EC1；
(2)如果AB＝2，AE＝
，OE⊥EC1，求AA1的长．
（1）见解析（2）3
【解析】(1)连接AC，A1C1.由底面是正方形知，BD⊥AC.
因为AA1⊥平面ABCD，BD?平面ABCD，所以AA1⊥BD.
又AA1∩AC＝A，所以BD⊥平面AA1C1C.
因为EC1?平面AA1C1C知，BD⊥EC1.
(2)设AA1的长为h，连结OC1.
在Rt△OAE中，AE＝
，AO＝
，
故OE2＝(
)2＋(
)2＝4.
在Rt△EA1C1中，A1E＝h－
，A1C1＝2
，
故E
＝(h－
)2＋(2
)2.
在Rt△OCC1中，OC＝
，CC1＝h，O＝h2＋(
)2.
因为OE⊥EC1，所以OE2＋E
＝O
，即
4＋(h－
)2＋(2
)2＝h2＋(
)2，
解得h＝3
，所以AA1的长为3.
练习册系列答案
相关题目
