题目内容
已知函数f(x)的定义域是(-∞,0)∪(0,+∞),对定义域内的任意m,n都有f(m•n)=f(m)+f(n),且当x>1时f(x)>0,f(2)=2,
(1)求证:f(x)是偶函数;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)解不等式f(2x-1)<4.
(1)证明:因为对定义域内的任意m,n都有f(m•n)=f(m)+f(n),
所以,令m=n=1,则f(1)=f(1)+f(1),即f(1)=0;
令m=n=-1,则f(1)=f(-1)+f(-1),即0=2f(-1),所以f(-1)=0.
对定义域内的任意m,取n=-1,有f(-m)=f(m)+f(-1),即f(-m)=f(m),
所以f(x)是偶函数.
(2)证明:设0<x1<x2,
则f(x2)-f(x1)=f(x1• )-f(x1)=f(x1)+f(
)-f(x1)=f(x1)+f( )-f(x1)=f(
)-f(x1)=f( ),
),
因为当x>1时f(x)>0,且 >1,所以f(
>1,所以f( )>0,
)>0,
即f(x2)-f(x1)>0,f(x2)>f(x1).
所以f(x)在(0,+∞)上是增函数;
(3)解:由f(2)=2,得4=f(2)+f(2)=f(2•2)=f(4),
由(1),(2)得,f(2x-1)<4?f(|2x-1|)<f(4)?0<|2x-1|<4,
解得- <x<
<x< ,且x
,且x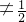 .
.
所以不等式的解集为:{x|- <x<
<x< ,且x
,且x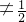 }.
}.
分析:(1)令m=n=1可求得f(1),令m=n=-1可求f(-1),在f(m•n)=f(m)+f(n)中,令n=-1,可得结论;
(2)设0<x1<x2,f(x2)-f(x1)=f(x1• )-f(x1),
)-f(x1),
依据f(m•n)=f(m)+f(n)及x>1时f(x)>0,可得f(x2)-f(x1)的符号,从而得证;
(3)由(1),(2)及已知f(2)=2,f(2x-1)<4?f(|2x-1|)<f(4)?0<|2x-1|<4,从而可解.
点评:本题考查抽象函数的奇偶性、单调性及其应用,定义是解决该类题目的基本方法.
所以,令m=n=1,则f(1)=f(1)+f(1),即f(1)=0;
令m=n=-1,则f(1)=f(-1)+f(-1),即0=2f(-1),所以f(-1)=0.
对定义域内的任意m,取n=-1,有f(-m)=f(m)+f(-1),即f(-m)=f(m),
所以f(x)是偶函数.
(2)证明:设0<x1<x2,
则f(x2)-f(x1)=f(x1•
 )-f(x1)=f(x1)+f(
)-f(x1)=f(x1)+f( )-f(x1)=f(
)-f(x1)=f( ),
),因为当x>1时f(x)>0,且
 >1,所以f(
>1,所以f( )>0,
)>0,即f(x2)-f(x1)>0,f(x2)>f(x1).
所以f(x)在(0,+∞)上是增函数;
(3)解:由f(2)=2,得4=f(2)+f(2)=f(2•2)=f(4),
由(1),(2)得,f(2x-1)<4?f(|2x-1|)<f(4)?0<|2x-1|<4,
解得-
 <x<
<x< ,且x
,且x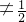 .
.所以不等式的解集为:{x|-
 <x<
<x< ,且x
,且x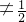 }.
}.分析:(1)令m=n=1可求得f(1),令m=n=-1可求f(-1),在f(m•n)=f(m)+f(n)中,令n=-1,可得结论;
(2)设0<x1<x2,f(x2)-f(x1)=f(x1•
 )-f(x1),
)-f(x1),依据f(m•n)=f(m)+f(n)及x>1时f(x)>0,可得f(x2)-f(x1)的符号,从而得证;
(3)由(1),(2)及已知f(2)=2,f(2x-1)<4?f(|2x-1|)<f(4)?0<|2x-1|<4,从而可解.
点评:本题考查抽象函数的奇偶性、单调性及其应用,定义是解决该类题目的基本方法.

练习册系列答案
相关题目
