题目内容
1.如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,AB⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.

(1)证明:BE∥平面PAD;
(2)平面EBD能垂直于平面ABCD吗,为什么?
2.在本题中,若平面EBD⊥平面ABCD,则四边形ABCD需满足什么说明条件?
答案:
解析:
提示:
解析:
|
1.(1)证明:如图,取PD的中点F,连结EF、AF,则EF∥CD,且CD=2EF.
又∵AB∥CD,CD=2AB,∴EF∥AB且EF=AB. ∴四边形ABEF是平行四边形. ∴AF∥BE.而AF (2)解:如图假设平面EBD能垂直于底面ABCD,过点E作EO⊥BD于点O,连结AO、CO.
∵面BDE∩面ABCD=BD,且EO 又∵PA⊥面ABCD,直线AC是PC在面ABCD上的射影, ∴平面ABCD的一条斜线PC上点E在面ABCD内的射影O在直线AC上. 同时,EO∥PA.又E为PC的中点, ∴O为AC的中点.由AB∥CD可知△ABO∽△CDO,且相似比为 ∴AB=CD.这与已知条件四边形ABCD为梯形,且CD=2AB矛盾. ∴假设“平面BDE⊥平面ABCD”是不成立的. 因此,平面BDE不能垂直于平面ABCD. 2.四边形ABCD为平行四边形. 思路分析:证线面平行,只要证出线平行于面内的一条直线即可.由E为PC的中点,所以取PD的中点F. |
提示:
|
解答探索性问题时,可从假设命题成立入手,若导出矛盾,说明假设不成立;若导不出矛盾,说明假设成立. |

练习册系列答案
相关题目


 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB. 如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E.
如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.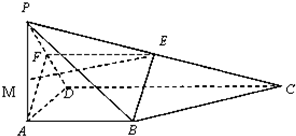 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=