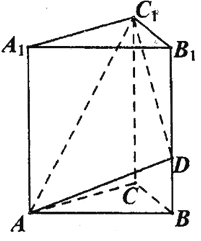
题目内容
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() (2)2
(2)2
【解析】
(1)先求导![]() ,将
,将![]() 代入导函数
代入导函数![]() 得切线斜率,将
得切线斜率,将![]() 代入原函数
代入原函数![]() 得切点纵坐标,再运用点斜式求出切线方程;
得切点纵坐标,再运用点斜式求出切线方程;
(2)法一:可知![]() ,先分离参数
,先分离参数![]() ,构造新函数
,构造新函数![]() 和
和![]() ,求出
,求出![]() 单调性,通过求出
单调性,通过求出![]() 的最值,便得到
的最值,便得到![]() 的最大值.
的最大值.
法二:先通过构造新函数![]() ,求出单调区间,再用分离参数
,求出单调区间,再用分离参数![]() ,利用基本不等式求出
,利用基本不等式求出![]() 的最大值.
的最大值.
(1)∵![]() ,
,![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
∴![]() ∴
∴![]()
解得![]()
(2)解法1:∵![]() ,由
,由![]()
∴![]()
令![]() ,则
,则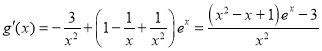
令![]() ,则
,则![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]()
∴![]() ,使得
,使得![]() ,即
,即![]()
∴![]()
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
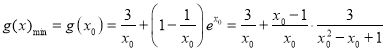
 ,∵
,∵![]() ∴
∴![]()
∴![]()
∵![]() ,∴整数
,∴整数![]() 的最大值为2
的最大值为2
解法2:令![]()
![]() 显然
显然![]() 在
在![]() 上递增
上递增
当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() ,合题意
,合题意
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]()
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
即![]() ,而
,而![]() 恒成立
恒成立
∴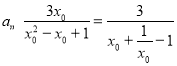
∵![]() ,
,![]() ,∴
,∴![]() .又∵
.又∵![]() .
.
若![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,不合题意舍去.
,不合题意舍去.
若![]() .
.
![]() ,
,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
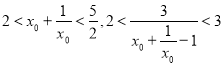
∴![]() ,合题意
,合题意
∴整数![]() 的最大值为2.
的最大值为2.

【题目】一只红玲虫的产卵数![]() 和温度
和温度![]() 有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在![]() 时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了![]() 与
与![]() 的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立![]() 与
与![]() 的指数回归方程
的指数回归方程![]() ,然后通过对数变换
,然后通过对数变换![]() ,把指数关系变为
,把指数关系变为![]() 与
与![]() ;模型②:先建立
;模型②:先建立![]() 与
与![]() 的二次回归方程
的二次回归方程![]() ,然后通过变换
,然后通过变换![]() ,把二次关系变为
,把二次关系变为![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() .
.
(1)分别利用这两个模型,求一只红玲虫在![]() 时产卵数的预测值;
时产卵数的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和![]() ,模型①的相关指数
,模型①的相关指数![]() ;模型②的残差平方和
;模型②的残差平方和![]() ,模型②的相关指数
,模型②的相关指数![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
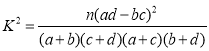 (其中
(其中![]() ).
).