题目内容
已知2x≤256且log2x≥
,求函数f(x)=log2
•log
的值域.
| 1 |
| 2 |
| x |
| 2 |
| 2 |
| ||
| 2 |
由2x≤256得x≤8,则
≤log2x≤3,
y=f(x)=(log2x-1)(log2x-2)=(log2x)2-3log2x+2,
令log2x=t,则t∈[
,3],
则y=t2-3t+2,其中对称轴为t=
,故当t=
时,y有最小值是-
,
故t=3时,y最大值2,故函数值域是[-
,2].
| 1 |
| 2 |
y=f(x)=(log2x-1)(log2x-2)=(log2x)2-3log2x+2,
令log2x=t,则t∈[
| 1 |
| 2 |
则y=t2-3t+2,其中对称轴为t=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
故t=3时,y最大值2,故函数值域是[-
| 1 |
| 4 |

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
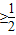 ,
,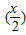 •log
•log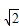
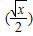 的最大值和最小值.
的最大值和最小值.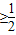 ,
, •log
•log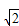
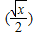 的最大值和最小值.
的最大值和最小值.