题目内容
在平面直角坐标系中,已知三点A(m,n),B(n,t),C(t,m),直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,而直线AB恰好经过抛物线x2=2p(y-q),(p>0)的焦点F并且与抛物线交于P、Q两点(P在y轴左侧).则|
|=( )
| 5 |
| 3 |
| PF |
| QF |
| A.9 | B.4 | C.
| D.
|
设kAB=
,kAC=
,
则
+
=
,
∵(n-m)•kAB=t-n=(t-m)+(m-n),
∴
=-
,
∴kAB-
=
,解得kAB=-
或2(舍去),
∵直线AB过抛物线x2=2p(y-q)的焦点,和直线AB过抛物线x2=2py的焦点,对|
|的值没有影响,故可研究AB过抛物线x2=2py的情况,
∴直线AB的方程为y=-
x+
,与抛物线联立消去y,
整理得x2+
x-p2=0,求得x=-
或
.
∵抛物线x2=2py的焦点为(0,
),设P(x1,y1),Q(x2,y2),P在y轴左侧,
∴x1=-
,x2=
∴|PF|=
(|x1-0|)=
|x1|,|QF|=
(|x1-0|)=
x2,
∴|
|=|
|=|
|=|
|=9.
故选:A.
| t-n |
| n-m |
| m-n |
| t-m |
则
| t-n |
| n-m |
| m-n |
| t-m |
| 5 |
| 3 |
∵(n-m)•kAB=t-n=(t-m)+(m-n),
∴
| m-n |
| t-m |
| 1 |
| kAB+1 |
∴kAB-
| 1 |
| kAB+1 |
| 5 |
| 3 |
| 4 |
| 3 |
∵直线AB过抛物线x2=2p(y-q)的焦点,和直线AB过抛物线x2=2py的焦点,对|
| PF |
| QF |
∴直线AB的方程为y=-
| 4 |
| 3 |
| p |
| 2 |
整理得x2+
| 8p |
| 3 |
| 9p |
| 3 |
| p |
| 3 |
∵抛物线x2=2py的焦点为(0,
| p |
| 2 |
∴x1=-
| 9p |
| 3 |
| p |
| 3 |
∴|PF|=
| 1+k2 |
| 1+k2 |
| 1+k2 |
| 1+k2 |
∴|
| PF |
| QF |
| ||
|
| x1 |
| x2 |
-
| ||
|
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

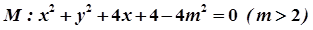 上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C.
上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C.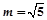 时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,
时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,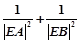 为定值?若存在,求出定点和定值;若不存在,请说明理由.
为定值?若存在,求出定点和定值;若不存在,请说明理由.