题目内容
在数列{an}和{bn}中，bn是an和an+1的等差中项，a1=2且对任意n∈N*都有3an+1-an=0，则{bn}的通项bn=______．
因为3an+1-an=0?
=
(n∈N*)．
∴{an}是公比为
的等比数列
?an=2•(
)n-1?
bn=
(an+an+1)=
[2•(
)n-1+2•(
)n]=
(
)n-1．
故答案为：
(
)n-1．
| an+1 |
| an |
| 1 |
| 3 |
∴{an}是公比为
| 1 |
| 3 |
?an=2•(
| 1 |
| 3 |
bn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
故答案为：
| 4 |
| 3 |
| 1 |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
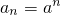，bn=（a+1）n+b，n=1，2，3，…，其中a≥2且a∈N*，b∈R．
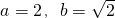时，数列{bn}中的任意三项都不能构成等比数列．
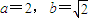时，数列{bn}中的任意三项都不能构成等比数列；