题目内容
设奇函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式
＜0的解集是______．
| f(x)-f(-x) |
| x |
∵函数f（x）是奇函数
∴f（-x）=-f（x）
∴不等式
| f(x)-f(-x) |
| x |
f（x）x＜0
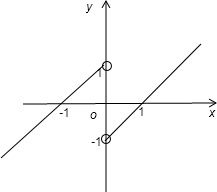
根据条件可作一函数图象：
∴不等式
| f(x)-f(-x) |
| x |
故答案为：（-1，0）∪（0，1）
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设奇函数f（x）在[-1，1]上是增函数，且f（-1）=-1，若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，则当a∈[-1，1]时，t的取值范围是（ ）
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|