题目内容
如图所示,四边形ABCD是边长为1 的 正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?
若存在,求线段AS的长;若不存在,请说明理由.

解析:(1)以D为坐标原点,建立空间直角坐标![]()
依题意,得![]() 。
。
![]()
![]() ,…………5分
,…………5分
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() …………6分
…………6分
(2)假设在线段![]() 上存在点
上存在点![]() ,使得
,使得![]()
![]() 平面
平面![]() .
.
![]() ,可设
,可设![]()
又![]() ……….9分
……….9分
由![]() 平面
平面![]() ,得
,得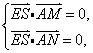 即
即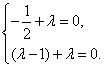
故![]() ,此时
,此时![]() .
.
经检验,当![]() 时,
时,![]() 平面
平面![]() .…………13分
.…………13分
故线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() …………14分
…………14分

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
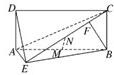 如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE. 如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC. 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.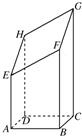 如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题: 如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,
如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,