题目内容
13.已知a>0,且二项式${(a\sqrt{x}-\frac{1}{{\sqrt{x}}})^6}$展开式中含$\frac{1}{x}$项的系数是135,则a=3.分析 由条件利用二项展开式的通项公式,求得展开式中含$\frac{1}{x}$项的系数,再根据展开式中含$\frac{1}{x}$项的系数为135,从而求得a的值.
解答 解:二项式${(a\sqrt{x}-\frac{1}{{\sqrt{x}}})^6}$展开式的通项公式为 Tr+1=${C}_{6}^{r}$•(-1)r•a6-r•x3-r,
令3-r=-1,求得r=4,故开式中含$\frac{1}{x}$项的系数是${C}_{6}^{4}$•a2=135,求得a=3,
故答案为:3.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
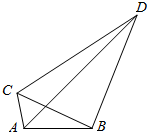 如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.
如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.