题目内容
9．化简：tanα+$\sqrt{\frac{1}{co{s}^{2}α}-1}$+2sin2α+2cos2α，其中α是第四象限角．分析 利用同角三角函数的基本关系、二倍角公式，以及三角函数在各个象限中的符号，化简所给的式子，可得结果．
解答 解：∵α是第四象限角，∴tanα+$\sqrt{\frac{1}{co{s}^{2}α}-1}$+2sin2α+2cos2α
=tanα+|$\frac{sinα}{cosα}$|+2•$\frac{1-cos2α}{2}$+cos2α+1
=tanα-tanα+2=2．
点评 本题主要考查同角三角函数的基本关系、二倍角公式，以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
相关题目
14．已知圆的方程为x2+y2=1，则圆心到直线x+y+2=0的距离为（ ）
| A． | 1 | B． | 2 | C． | 2$\sqrt{2}$ | D． | $\sqrt{2}$ |
18．
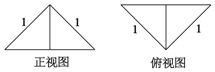把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图与俯视图如图所示，则其侧视图的面积为（ ）
把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图与俯视图如图所示，则其侧视图的面积为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{1}{4}$ |
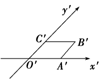在直观图（如图所示）中，四边形O'A'B'C'为菱形且边长为2cm，则在xOy坐标系中，四边形OABC的面积为8cm2．