题目内容
设函数f（x）=x2+x+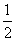
的定义域是［n，n+1］（n∈N），问f（x）的值域中有多少个整数？
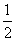的定义域是［n，n+1］（n∈N），问f（x）的值域中有多少个整数？ 解：∵f（x）=（x+
）2+
的图象是以（-
，
）为顶点，开口向上的抛物线，
而自然数n＞-
，
∴f（x）的值域是［f（n），f（n+1）］，即［n2+n+，n2+3n+
］，
其中最小的整数是n2+n+1，最大的整数是n2+3n+2，
共有（n2+3n+2）-（n2+n+1）+1=2n+2个整数。
）2+的图象是以（-，）为顶点，开口向上的抛物线，而自然数n＞-
，∴f（x）的值域是［f（n），f（n+1）］，即［n2+n+
，n2+3n+］，其中最小的整数是n2+n+1，最大的整数是n2+3n+2，
共有（n2+3n+2）-（n2+n+1）+1=2n+2个整数。
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目