题目内容
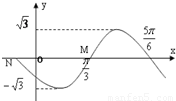
图为f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜π）的图象的一段，则其解析式为（ ）
A．
B．
C．
D．
【答案】分析：由已知中函数的图象，我们可以求出函数的最大值，最小值，进而确定A值，还可以确定函数的周期进而得到ω值，求出最大值的坐标后，代入可求出φ值，进而得到函数的解析式．
解答：解：由已知图象可得
函数的最大值为
，最小值为-
，故A=3
周期T=2（
-
）=π，故ω=2
则f（x）=
sin（2x+ϕ）
又由函数的最大值点为（
，
）
则
+ϕ=
故φ=
故f（x）=
sin（2x
）
故选B
点评：本题考查的知识点是正弦型函数解析式的求法，其中根据函数的图象确定出函数的最值，周期，最值点坐标，进而得到A，ω，φ值是解答本题的关键．
解答：解：由已知图象可得
函数的最大值为
，最小值为-，故A=3周期T=2（
-）=π，故ω=2则f（x）=
sin（2x+ϕ）又由函数的最大值点为（
，）则
+ϕ=故φ=
故f（x）=
sin（2x）故选B
点评：本题考查的知识点是正弦型函数解析式的求法，其中根据函数的图象确定出函数的最值，周期，最值点坐标，进而得到A，ω，φ值是解答本题的关键．
练习册系列答案
相关题目
如图为f（x）=Asin（ωx+?）（A＞0，?＞0，?∈（-π，0））的图象的一段，
图为f（x）=Asin（ωx+?）（A＞0，ω＞0，|?|＜π）的图象的一段，则其解析式为（ ）
个单位，得到函数g（x）的图象，求函数g（x）在
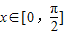的值域．
