题目内容
定义在（-1，1）上的函数f（x）满足
（ⅰ）对任意x、y∈（-1，1）有f（x）+f（y）=f（
）
（ⅱ）当x∈（-1，0）时，有f（x）＞0，试研究f（
）+f（
）+…+f（
）与f（
）的关系．
（ⅰ）对任意x、y∈（-1，1）有f（x）+f（y）=f（
| x+y |
| 1+xy |
（ⅱ）当x∈（-1，0）时，有f（x）＞0，试研究f（
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
在（ⅰ）中，令x=y=0，可得到f（0）+f（0）=f（0），可得f（0）=0，
令x=-y，可得f（x）+f（-x）=f（0），
则f（x）+f（-x）=0，
故f（x）是奇函数；
又由（ii），当x∈（-1，0）时，有f（x）＞0，
当x∈（0，1）时，则-x∈（-1，0）
f（x）=-f（-x）＜0，
即当x∈（0，1）时，f（x）＜0，
f（
）=f（
）+f（-
）=f（
）-f（
）
则f（
）+f（
）+…+f（
）=[f（
）-f（
）]+[f（
）-f（
）]+…+[f（
）-f（
）]
=f（
）-f（
）；
∵0＜
＜1，
∴f（
）＜0；
则f（
）-f（
）＞f（
），
故f（
）+f（
）+…+f（
）＞f（
）．
令x=-y，可得f（x）+f（-x）=f（0），
则f（x）+f（-x）=0，
故f（x）是奇函数；
又由（ii），当x∈（-1，0）时，有f（x）＞0，
当x∈（0，1）时，则-x∈（-1，0）
f（x）=-f（-x）＜0，
即当x∈（0，1）时，f（x）＜0，
f（
| 1 |
| n2+3n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
则f（
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=f（
| 1 |
| 2 |
| 1 |
| n+2 |
∵0＜
| 1 |
| n+2 |
∴f（
| 1 |
| n+2 |
则f（
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| 2 |
故f（
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
＞0.
)＜f(
).
是定义在（-1，1）的奇函数，且f（
）=
．
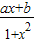是定义在（-1，1）的奇函数，且f（
）=
．