题目内容
【题目】已知函数f(x)=2cosx(sinx+cosx),x∈R.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
【答案】解:( I)函数f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+cos2x+1= ![]() sin(2x+
sin(2x+ ![]() )+1,∴函数f(x)的最小正周期为:T=
)+1,∴函数f(x)的最小正周期为:T= ![]() =π;
=π;
(Ⅱ) 由 ![]() ,解得
,解得 ![]() ,∴函数f(x)的单调递增区间为
,∴函数f(x)的单调递增区间为![]() (k∈Z);
(k∈Z);
( III)由 ![]() ,得
,得 ![]() ,令2x+
,令2x+ ![]() =﹣
=﹣ ![]() ,解得x=﹣
,解得x=﹣ ![]() ,∴f(x)min=
,∴f(x)min= ![]() =
= ![]() ×(﹣
×(﹣ ![]() )+1=0,
)+1=0,
令2x+ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,∴f(x)max=
,∴f(x)max= ![]() =
= ![]() ×1+1=
×1+1= ![]() +1.
+1.
【解析】( I)根据正弦函数和余弦函数的二倍角化简成正弦型函数可得周期。(Ⅱ)把![]() 看成一个整体代入正弦函数的单调区间整理即得。(Ⅲ)由整体思想可得
看成一个整体代入正弦函数的单调区间整理即得。(Ⅲ)由整体思想可得 ![]() ≤ 2 x +
≤ 2 x + ![]() ≤
≤ ![]() 根据正弦函数的单调性可得 ,最小值当整体取-
根据正弦函数的单调性可得 ,最小值当整体取-![]() 时得到,最大值 当整体取
时得到,最大值 当整体取![]() 时得到。
时得到。
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 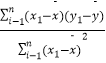 =
= 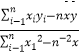 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?