题目内容
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
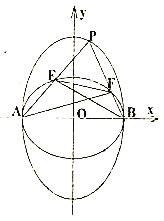
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于两点
交于两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
【答案】(1) ![]() ;(2) 详见解析.
;(2) 详见解析.
【解析】试题分析:(1)由题意可得:a=2c,又a2=3+c2,解得a2即可得出椭圆M的方程;(2)设直线PQ的方程为:y=k(x-4)(k≠0),代入椭圆方程可得:(3+4k2)x2-32k2x+64k2-12=0,设P(x1,y1),Q(x2,y2),E(x2,-y2),直线PE的方程为: ![]() ,令y=0,可得
,令y=0,可得![]() ,把根与系数的关系代入即可证明.
,把根与系数的关系代入即可证明.
试题解析:
(1)由题意得椭圆![]() 的焦点在
的焦点在![]() 轴上,∵椭圆
轴上,∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,解得
,解得![]() .∴椭圆
.∴椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:易知直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ,由
,由![]() 得,
得, ![]() .设
.设![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .令
.令![]() 得
得![]()
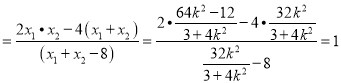 ,∴直线
,∴直线![]() 过定点
过定点![]() ,又
,又![]() 的右焦点为
的右焦点为![]() ,∴直线
,∴直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.

练习册系列答案
相关题目