题目内容
已知函数f(x)=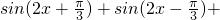 2cos2x-1,x∈R.
2cos2x-1,x∈R.
(Ⅰ)求函数f(x)的值域;
(Ⅱ)求函数f(x)的单调递增区间.
解:(Ⅰ)f(x)=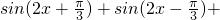 2cos2x-1
2cos2x-1
=( sin2x+
sin2x+ cos2x)+(
cos2x)+( sin2x-
sin2x- cos2x)+cos2x
cos2x)+cos2x
=sin2x+cos2x= sin(2x+
sin(2x+ )…(3分)
)…(3分)
由于x∈R,得2x+ ∈R,故sin(2x+
∈R,故sin(2x+ )∈[-1,1],
)∈[-1,1],
∴函数的值域为y∈[- ,
, ]…(6分)
]…(6分)
(Ⅱ)令- +2kπ<2x+
+2kπ<2x+ <
< +2kπ,k∈Z,…(8分)
+2kπ,k∈Z,…(8分)
解得- +kπ<x<
+kπ<x< +kπ,k∈Z,…(10分)
+kπ,k∈Z,…(10分)
∴f(x)的递增区间为(- +kπ,
+kπ, +kπ),k∈Z,…(12分)
+kπ),k∈Z,…(12分)
注意:写成[- +kπ,
+kπ, +kπ],k∈Z,也是正确答案.
+kπ],k∈Z,也是正确答案.
分析:(I)利用两角和与差的正弦公式、二倍角的余弦公式进行展开,合并同类项,再用辅助角公式化简得f(x)= sin(2x+
sin(2x+ ),再用三角函数的图象与性质,可求函数f(x)的值域.
),再用三角函数的图象与性质,可求函数f(x)的值域.
(II)由正弦函数的单调区间的公式,建立关于x的不等式并解之,得- +kπ<x<
+kπ<x< +kπ,k∈Z,再将其变成区间就是要求的函数单调增区间.
+kπ,k∈Z,再将其变成区间就是要求的函数单调增区间.
点评:本题给出三角函数式,要我们通过化简求其单调区间与值域,着重考查了三角恒等变形和三角函数的图象与性质等知识,属于基础题.
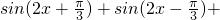 2cos2x-1
2cos2x-1=(
 sin2x+
sin2x+ cos2x)+(
cos2x)+( sin2x-
sin2x- cos2x)+cos2x
cos2x)+cos2x=sin2x+cos2x=
 sin(2x+
sin(2x+ )…(3分)
)…(3分)由于x∈R,得2x+
 ∈R,故sin(2x+
∈R,故sin(2x+ )∈[-1,1],
)∈[-1,1],∴函数的值域为y∈[-
 ,
, ]…(6分)
]…(6分)(Ⅱ)令-
 +2kπ<2x+
+2kπ<2x+ <
< +2kπ,k∈Z,…(8分)
+2kπ,k∈Z,…(8分)解得-
 +kπ<x<
+kπ<x< +kπ,k∈Z,…(10分)
+kπ,k∈Z,…(10分)∴f(x)的递增区间为(-
 +kπ,
+kπ, +kπ),k∈Z,…(12分)
+kπ),k∈Z,…(12分)注意:写成[-
 +kπ,
+kπ, +kπ],k∈Z,也是正确答案.
+kπ],k∈Z,也是正确答案.分析:(I)利用两角和与差的正弦公式、二倍角的余弦公式进行展开,合并同类项,再用辅助角公式化简得f(x)=
 sin(2x+
sin(2x+ ),再用三角函数的图象与性质,可求函数f(x)的值域.
),再用三角函数的图象与性质,可求函数f(x)的值域.(II)由正弦函数的单调区间的公式,建立关于x的不等式并解之,得-
 +kπ<x<
+kπ<x< +kπ,k∈Z,再将其变成区间就是要求的函数单调增区间.
+kπ,k∈Z,再将其变成区间就是要求的函数单调增区间.点评:本题给出三角函数式,要我们通过化简求其单调区间与值域,着重考查了三角恒等变形和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目